题目内容
14．为强化安全意识，某学校拟在未来的连续5天中随机抽取2天进行紧急疏散演练，那么选择的2天恰好为连续2天的概率是$\frac{2}{5}$（结果用最简分数表示）．分析 某学校拟在未来的连续5天中随机抽取2天进行紧急疏散演练，先求出基本事件总数，再求出选择的2天恰好为连续2天包含的基本事件个数，由此能求出选择的2天恰好为连续2天的概率．
解答 解：某学校拟在未来的连续5天中随机抽取2天进行紧急疏散演练，
基本事件总数为n=${C}_{5}^{2}$=10，
选择的2天恰好为连续2天包含的基本事件个数m=4，
∴选择的2天恰好为连续2天的概率p=$\frac{m}{n}=\frac{4}{10}=\frac{2}{5}$．
故答案为：$\frac{2}{5}$．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
相关题目
4．将函数$f（x）=sin（{x+\frac{π}{6}}）$的图象上各点的纵坐标不变，横坐标扩大到原来的2倍，所得函数g（x）图象的一个对称中心可以是（ ）
| A． | $（{-\frac{π}{12}，0}）$ | B． | $（{\frac{5π}{12}，0}）$ | C． | $（{-\frac{π}{3}，0}）$ | D． | $（{\frac{2π}{3}，0}）$ |
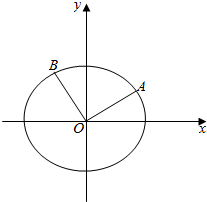如图，已知点A是单位圆上一点，且位于第一象限，以x轴的正半轴为始边，OA为终边的角设为α，将OA绕坐标原点逆时针旋转$\frac{π}{2}$至OB．
3．若函数f（x）=$\frac{2}{3}$x3-ax2+6x-3在[1，2]上单调递增，则实数a的最大值为（ ）
| A． | 2$\sqrt{3}$ | B． | $\sqrt{3}$ | C． | 4 | D． | $\frac{7}{2}$ |