题目内容
已知函数f(x)=ax-ex(a>0).
(1)若a=
,求函数f(x)在x=1处的切线方程;
(2)当1≤a≤e+1时,求证:f(x)≤x.
(1)若a=
| 1 |
| 2 |
(2)当1≤a≤e+1时,求证:f(x)≤x.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)根据导数的几何意义,曲线f(x)在x=x0处的切线方程为y-f(x0)=f'(x0)(x-x0),代入计算即可.
(2)作差并将x-f(x)=-ax+x+ex看成是关于a的函数g(a),要证明不等式成立,只需证明g(a)≥0对于一切1≤a≤e+1恒成立即可,亦即证明
.
(2)作差并将x-f(x)=-ax+x+ex看成是关于a的函数g(a),要证明不等式成立,只需证明g(a)≥0对于一切1≤a≤e+1恒成立即可,亦即证明
|
解答:
解:(1)当a=
时,f(x)=
x-ex,f(1)=
-e,
f′(x)=
-ex,f′(1)=
-e,
故函数f(x)在x=1处的切线方程为y-
+e=(
-e)(x-1),
即(
-e)x-y=0
(2)令g(a)=x-f(x)=-ax+x+ex,
只需证明g(a)≥0在1≤a≤e+1时恒成立,
一方面,g(1)=-x+x+ex=ex>0①
另一方面,g(1+e)=-x(1+e)+x+ex=ex-ex,
设h(x)=ex-ex,则h′(x)=ex-e,
当x<1时,h′(x)<0;当x>1时,h′(x)>0.
∴h(x)在(-∞,1)单调递减;在(1,+∞)单调递增.
∴h(x)≥h(1)=e-e•1=0,即g(1+e)≥0②
由①②知,g(a)≥0在1≤a≤e+1时恒成立
故当1≤a≤e+1时,f(x)≤x.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
f′(x)=
| 1 |
| 2 |
| 1 |
| 2 |
故函数f(x)在x=1处的切线方程为y-
| 1 |
| 2 |
| 1 |
| 2 |
即(
| 1 |
| 2 |
(2)令g(a)=x-f(x)=-ax+x+ex,
只需证明g(a)≥0在1≤a≤e+1时恒成立,
一方面,g(1)=-x+x+ex=ex>0①
另一方面,g(1+e)=-x(1+e)+x+ex=ex-ex,
设h(x)=ex-ex,则h′(x)=ex-e,
当x<1时,h′(x)<0;当x>1时,h′(x)>0.
∴h(x)在(-∞,1)单调递减;在(1,+∞)单调递增.
∴h(x)≥h(1)=e-e•1=0,即g(1+e)≥0②
由①②知,g(a)≥0在1≤a≤e+1时恒成立
故当1≤a≤e+1时,f(x)≤x.
点评:本题中涉及到高考常考内容,即导数的几何意义,一般会以填空选择题的形式呈现,属于容易题;第二问中的证明中,由1≤a≤e+1知,需要将函数看成关于a的函数,再通过相关函数知识解决,学生在处理时,往往容易把它当成关于x的函数,从而没法继续证明.所以,在解题时看根据题目给的条件,分辨哪个是自变量,哪个是参数,是至关重要的.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
下列说法正确的是( )
| A、若已知两个变量具有线性相关关系,且它们正相关,则其线性回归直线的斜率为正 |
| B、直线l垂直于平面α的充要条件为l垂直于平面α内的无数条直线 |
| C、若随机变量ξ~N(10,0.12),且P(9.9<ξ<10.1)=0.6826,则P(ξ>10.1)=0.3174 |
| D、已知命题P:?x∈R,x2-2x+2>0,则¬p:?x∈R,x2-2x+2<0 |
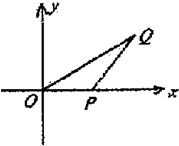 如图已知△OPQ的面积为S,且
如图已知△OPQ的面积为S,且