题目内容
平面直角坐标系有两点P(1,cosx),Q(cosx,1),其中x∈[-
,
];
(1)求向量
和
的夹角θ的余弦用x表示的函数f(x);
(2)求题(1)中f(x)的值域.
| π |
| 4 |
| π |
| 4 |
(1)求向量
| OP |
| OQ |
(2)求题(1)中f(x)的值域.
考点:平面向量数量积的运算,三角函数中的恒等变换应用
专题:三角函数的图像与性质,平面向量及应用
分析:(1)由已知求出向量
和
的坐标,代入cosθ=
求出f(x);
(2)由(1)可求得f(x)=
=
由x的范围可求cosθ的范围,结合函数的单调性即可求cosθ的最小值.
| OP |
| OQ |
| ||||
|
|
(2)由(1)可求得f(x)=
| 2cosx |
| 1+cos2x |
| 2 | ||
cosx+
|
解答:
解:(1)由于
•
=2cosx…(2分)
|
|•|
|=1+cos2x…(4分)
∴cosθ=
=
=f(x)…(6分)
(2)∵x∈[-
,
]
∴cosx∈[
,1]
f(x)=
=
令g(x)=x+
…(8分)
设x1,x2∈[
,1],且x1<x2
g(x1)-g(x2)=x1+
-x2-
=(x1-x2)(
)<0
∴g(x)=x+
在[
,1]上是减函数. …(10分)
∴2≤cosx+
≤
≤f(x)≤1
即f(x)的值域是[
,1]. …(12分)
| OP |
| OQ |
|
| OP |
| OQ |
∴cosθ=
| ||||
|
|
| 2cosx |
| 1+cos2x |
(2)∵x∈[-
| π |
| 4 |
| π |
| 4 |
∴cosx∈[
| ||
| 2 |
f(x)=
| 2cosx |
| 1+cos2x |
| 2 | ||
cosx+
|
令g(x)=x+
| 1 |
| x |
设x1,x2∈[
| ||
| 2 |
g(x1)-g(x2)=x1+
| 1 |
| x1 |
| 1 |
| x2 |
| x1x2-1 |
| x1x2 |
∴g(x)=x+
| 1 |
| x |
| ||
| 2 |
∴2≤cosx+
| 1 |
| cosx |
3
| ||
| 2 |
2
| ||
| 3 |
即f(x)的值域是[
2
| ||
| 3 |
点评:本题主要考查了向量的数量积的性质的坐标表示,向量与 三角函数及函数的单调性等知识的综合应用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
过点(-2,4)且在两坐标轴上截距的绝对值相等的直线有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
 图是某赛季甲、乙两名篮球运动员每场比赛得分统计的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
图是某赛季甲、乙两名篮球运动员每场比赛得分统计的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )| A、62 | B、63 | C、64 | D、65 |
设(-∞,a)为f(x)=
反函数的一个单调递增区间,则实数a的取值范围为 ( )
| 1-2x |
| x-2 |
| A、a≤2 | B、a≥2 |
| C、a≤-2 | D、a≥-2 |
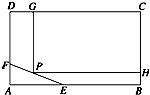 如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.
如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.