题目内容
甲、乙两台机床在相同的技术条件下,同时生产一种零件,现在从中抽测10个,它们的尺寸分别如下(单位:mm).
甲机床:10.2 10.1 10 9.8 9.9 10.3 9.7 10 9.9 10.1;
乙机床:10.3 10.4 9.6 9.9 10.1 10.9 8.9 9.7 10.2 10.
分别计算上面两个样本的平均数和方差,如图纸规定零件的尺寸为10mm,从计算的结果来看哪台机床加工这种零件较合适?
(样本数据x1,x2,…,xn的样本方差s2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],其中
为样本均数.)
甲机床:10.2 10.1 10 9.8 9.9 10.3 9.7 10 9.9 10.1;
乙机床:10.3 10.4 9.6 9.9 10.1 10.9 8.9 9.7 10.2 10.
分别计算上面两个样本的平均数和方差,如图纸规定零件的尺寸为10mm,从计算的结果来看哪台机床加工这种零件较合适?
(样本数据x1,x2,…,xn的样本方差s2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
考点:极差、方差与标准差,众数、中位数、平均数
专题:概率与统计
分析:分别求出两个样本的平均数和方差,由此从计算的结果来看甲台机床加工这种零件较合适.
解答:
解:
=
(10.2+10.1+10+9.8+9.9+10.3+9.7+10+9.9+10.1)=10,
=
(10.3+10.4+9.6+9.9+10.1+10.9+8.9+9.7+10.2+10)=10,
S甲2=
[(10.2-10)2+(10.1-10)2+(10-10)2+(9.8-10)2+(9.9-10)2+(10.3-10)2+(9.7-10)2+(10-10)2+(9.9-10)2+(10.1-10)2]=0.03,
S乙2=
[(10.3-10)2+(10.4-10)2+(9.6-10)2+(9.9-10)2+(10.1-10)2+(10.9-10)2+(8.9-10)2+(9.7-10)2+(10.2-10)2+(10-10)2]=0.258,
∵S甲2<S乙2,
∴计算的结果来看甲台机床加工这种零件较合适.
. |
| x甲 |
| 1 |
| 10 |
. |
| x乙 |
| 1 |
| 10 |
S甲2=
| 1 |
| 10 |
S乙2=
| 1 |
| 10 |
∵S甲2<S乙2,
∴计算的结果来看甲台机床加工这种零件较合适.
点评:本题考查样本的平均数和方差的求法,是基础题,解题时要认真审题,注意方差公式的合理运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
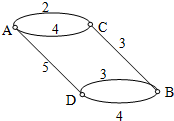 如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )
如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )| A、11 | B、10 | C、8 | D、7 |
如果a⊥b,那么a与b( )
| A、一定相交 | B、一定异面 |
| C、一定共面 | D、一定不平行 |