题目内容
17．（2-$\frac{1}{x}$）（1-2x）4的展开式中x2的系数为80．分析 把（1-2x）4按照二项式定理展开，可得（2-$\frac{1}{x}$）（1-2x）4的展开式中x2的系数．
解答 解：∵（2-$\frac{1}{x}$）（1-2x）4 =（2-$\frac{1}{x}$）•（1-${C}_{4}^{1}$•2x+${C}_{4}^{2}$•4x2-${C}_{4}^{3}$•8x3+${C}_{4}^{4}$•16x4），
故展开式中x2的系数为展开式中x2的系数为2•${C}_{4}^{2}$•4+（-1）•（-${C}_{4}^{3}$•8）=80，
故答案为：80．
点评 本题主要考查二项式定理的应用，二项式系数的性质，二项式展开式的通项公式，属于基础题．
练习册系列答案
相关题目
5．
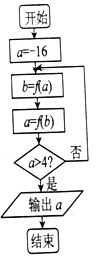在如图所示的程序框图中，若函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}（-x）（x＜0）}\\{{2}^{x}（x≥0）}\end{array}\right.$，则输出的结果是（ ）
在如图所示的程序框图中，若函数f（x）=$\left\{\begin{array}{l}{lo{g}_{\frac{1}{2}}（-x）（x＜0）}\\{{2}^{x}（x≥0）}\end{array}\right.$，则输出的结果是（ ）| A． | 16 | B． | 8 | C． | 216 | D． | 28 |
12．
如图，在平行四边形ABCD中，AB=1，AD=2，点E，F，G，H分别是AB，BC，CD，DA边上的中点，则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=（ ）
如图，在平行四边形ABCD中，AB=1，AD=2，点E，F，G，H分别是AB，BC，CD，DA边上的中点，则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=（ ）| A． | $\frac{3}{2}$ | B． | $-\frac{3}{2}$ | C． | $\frac{3}{4}$ | D． | $-\frac{3}{4}$ |
2．4张卡片上分别写有数字1，2，3，4，从这4张卡片中随机有放回的抽取2张，则取出的2张卡片上的数字之差的绝对值为奇数的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
6．阅读如图所示的程序框图，输入的s值为（ ）
| A． | 0 | B． | $1+\sqrt{2}$ | C． | $1+\frac{{\sqrt{2}}}{2}$ | D． | $\sqrt{2}-1$ |
7．△ABC的三内角A，B，C所对边的长分别是a，b，c，若$\frac{sinB-sinA}{sinC}=\frac{{\sqrt{2}a+c}}{a+b}$，则角B的大小为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{3π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |