题目内容
12. 如图,在平行四边形ABCD中,AB=1,AD=2,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=( )
如图,在平行四边形ABCD中,AB=1,AD=2,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=( )| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | $\frac{3}{4}$ | D. | $-\frac{3}{4}$ |
分析 将所求利用平行四边形的相邻两边对应向量表示,然后进行向量的运算.
解答 解:在平行四边形ABCD中,AB=1,AD=2,点E,F,G,H分别是AB,BC,CD,DA边上的中点,则$\overrightarrow{EF}=-\overrightarrow{GH}$,$\overrightarrow{FG}=-\overrightarrow{HE}$,
所以$\overrightarrow{EF}•\overrightarrow{FG}+\overrightarrow{GH}•\overrightarrow{HE}$=2$\overrightarrow{EF}•\overrightarrow{FG}$=$(\overrightarrow{AB}+\overrightarrow{BC})×\frac{1}{2}(\overrightarrow{AD}-\overrightarrow{AB})$=$\frac{1}{2}({\overrightarrow{AD}}^{2}-{\overrightarrow{AB}}^{2})$=$\frac{3}{2}$;
故选:A.
点评 本题考查了平面向量的运算;用到了三角形法则.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
7.设A,B分别是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右顶点,P是双曲线C上异于A,B的任一点,设直线AP,BP的斜率分别为m,n,则$\frac{2a}{b}$+ln|m|+ln|n|取得最小值时,双曲线C的离心率为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\sqrt{6}$ |
1.若如图所示的程序框图输出的y=2,可输入的x的值的个数为( )


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
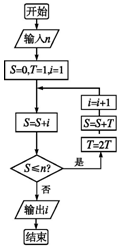 执行如图所示的程序框图,当输出i的值是4时,输入的整数n的最大值是23.
执行如图所示的程序框图,当输出i的值是4时,输入的整数n的最大值是23.