题目内容
20.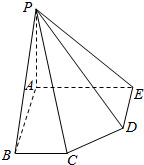 如图所示在五棱锥P-ABCDE中,侧棱PA⊥底面ABCDE,∠EAB=∠ABC=∠DEA=90°,AB=AE=2,BC=DE=1.求证:BD⊥平面PAC.
如图所示在五棱锥P-ABCDE中,侧棱PA⊥底面ABCDE,∠EAB=∠ABC=∠DEA=90°,AB=AE=2,BC=DE=1.求证:BD⊥平面PAC.
分析 以A为原点,分别以AE,AB,AP为x,y,z轴正方向建立空间直角坐标系,由题意可得向量$\overrightarrow{AC}$,$\overrightarrow{BD}$的坐标,可求$\overrightarrow{AC}$•$\overrightarrow{BD}$=0,从而证明AC⊥BD,又可证PA⊥BD,从而证明BD⊥平面PAC.
解答  证明:如图,以A为原点,分别以AE,AB,AP为x,y,z轴正方向建立空间直角坐标系,
证明:如图,以A为原点,分别以AE,AB,AP为x,y,z轴正方向建立空间直角坐标系,
∵侧棱PA⊥底面ABCDE,∠EAB=∠ABC=∠DEA=90°,AB=AE=2,BC=DE=1.
∴可得:A(0,0,0),C(1,2,0),B(0,2,0),D(2,1,0),
∴$\overrightarrow{AC}$=(1,2,0),$\overrightarrow{BD}$=(2,-1,0),
∵$\overrightarrow{AC}$•$\overrightarrow{BD}$=1×2-2×1+0×0=0,
∴AC⊥BD,
又∵侧棱PA⊥底面ABCDE,BD?底面ABCDE,
∴PA⊥BD,
∵AC∩PA=A,
∴BD⊥平面PAC.
点评 本题主要考查了直线与平面垂直的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.变量x,y具有线性相关关系,现测得一组数据如下:
根据如表,利用最小二乘法得到回归直线方程$\stackrel{∧}{y}$=0.7x+$\stackrel{∧}{a}$,据此判断,当x=5,时,$\stackrel{∧}{y}$与实际值y的大小关系为( )
| x | 2 | 3 | 4 | 5 |
| y | 2 | 2.5 | 3.5 | 4 |
| A. | $\stackrel{∧}{y}$>y | B. | $\stackrel{∧}{y}$>y | C. | $\stackrel{∧}{y}$=y | D. | 无法确定 |