题目内容
9．已知f（x）=$\left\{\begin{array}{l}{2x-1，x＜0}\\{3-x，x≥0}\end{array}\right.$，求f（x）＞-1的解．分析 根据不等式的解法，利用分类讨论即可得到结论．
解答 解：∵f（x）=$\left\{\begin{array}{l}{2x-1，x＜0}\\{3-x，x≥0}\end{array}\right.$，f（x）＞-1，
∴$\left\{\begin{array}{l}{x＜0}\\{2x-1＞-1}\end{array}\right.$或$\left\{\begin{array}{l}{x≥0}\\{3-x＞-1}\end{array}\right.$，
∴$\left\{\begin{array}{l}{x＜0}\\{x＞0}\end{array}\right.$，或$\left\{\begin{array}{l}{x≥0}\\{x＜4}\end{array}\right.$，
解得0≤x＜4，
故不等式的解集为[0，4）．
点评 本题主要考查不等式的解法，利用分类讨论是解决本题的关键，比较基础．
练习册系列答案
相关题目
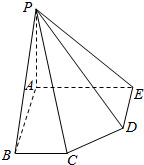如图所示在五棱锥P-ABCDE中，侧棱PA⊥底面ABCDE，∠EAB=∠ABC=∠DEA=90°，AB=AE=2，BC=DE=1．求证：BD⊥平面PAC．
4．不等式x（|x|-1）＜0的解集是（ ）
| A． | （-∞，-1）∪（0，1） | B． | （-∞，-1）∪（1，+∞） | C． | （-1，0）∪（1，+∞） | D． | （-1，0）∪（0，1） |