题目内容
15.已知直线y=kx(k>0)与圆C:(x-2)2+y2=1相交于A,B两点,若AB=$\frac{2}{5}$$\sqrt{5}$则k=$\frac{1}{2}$.分析 求出圆心到直线的距离d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$,利用勾股定理,建立方程,即可求出k.
解答 解:圆心到直线的距离d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$,
∵AB=$\frac{2}{5}$$\sqrt{5}$,
∴($\frac{|2k|}{\sqrt{{k}^{2}+1}}$)2+($\frac{\sqrt{5}}{5}$)2=1,
∴k=±$\frac{1}{2}$,
∵k>0,
∴k=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查直线与圆的位置关系,考查勾股定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.椭圆4x2+5y2=1的左、右焦点为F,F′,过F′的直线与椭圆交于M,N,则△MNF的周长为( )
| A. | 2 | B. | 4 | C. | $\frac{4\sqrt{5}}{5}$ | D. | 4$\sqrt{5}$ |
3.若两平行直线2x+y-4=0与y=-2x-m-2间的距离不大于$\sqrt{5}$,则m的取值范围是( )
| A. | [-11,-1] | B. | [-11,0] | C. | [-11,-6]∪(-6,-1] | D. | [-1,+∞) |
4.不等式x(|x|-1)<0的解集是( )
| A. | (-∞,-1)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-1,0)∪(0,1) |
 已知三棱柱ABC-A1B1C1,CB⊥平面BAA1B1,且四边形BAA1B1是正方形,M,N分别是AA1,BC的中点.
已知三棱柱ABC-A1B1C1,CB⊥平面BAA1B1,且四边形BAA1B1是正方形,M,N分别是AA1,BC的中点.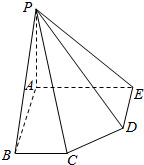 如图所示在五棱锥P-ABCDE中,侧棱PA⊥底面ABCDE,∠EAB=∠ABC=∠DEA=90°,AB=AE=2,BC=DE=1.求证:BD⊥平面PAC.
如图所示在五棱锥P-ABCDE中,侧棱PA⊥底面ABCDE,∠EAB=∠ABC=∠DEA=90°,AB=AE=2,BC=DE=1.求证:BD⊥平面PAC.