题目内容
11.已知数列{an}满足:an+1=2an,且a1,a2+1,a3成等差数列.(1)求数列{an}的通项公式;
(2)折bn=log2an(neN*),试求数列($\frac{1}{{b}_{n•{b}_{n+1}}}$)的前n项和Tn.
分析 (1)利用等差数列与等比数列的通项公式即可得出.
(2)利用对数的运算性质、“裂项求和”即可得出.
解答 解:(1)数列{an}满足:an+1=2an,且a1,a2+1,a3成等差数列.
∴2(a2+1)=a1+a3,
∴2a2+2=$\frac{{a}_{2}}{2}$+2a2,
解得a2=4.
∴an=${a}_{2}•{2}^{n-2}$=4•2n-2=2n.
(2)bn=log2an=n,
$\frac{1}{{b}_{n•{b}_{n+1}}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$.
∴数列{bn}前n项和Tn=$(1-\frac{1}{2})$+$(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$.
点评 本题考查了“裂项求和”、等差数列与等比数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
2.某军区老干部休养所(简称军干所)为纪念抗战胜利70周年,举行老干部捐赠抗战纪念品教育下一代的活动,随机抽取a名老干部为样本,得到这些老干部捐赠抗战纪念品的个数,根据此数据作出了频率分布表:
(1)求出表中m,n,p,a的值;
(2)军干所决定对捐赠抗战纪念品的老干部进行表彰,对捐赠抗战纪念品数在[16,20]区间的老干部发放价值400元的奖品,对捐赠抗战纪念品数在[11,15]区间的老干部发放价值300元的奖品,对捐赠抗战纪念品数在[6,10]区间的老干部发放价值200元的奖品,对捐赠抗战纪念品数在[1,5]区间的老干部发放价100元的奖品,在所取样本中,任意抽取2人,并设x为此二人所获得奖品价值之差的绝对值,求x的分布列与数学期望E(X).
| 分组 | 频数 | 频率 |
| [1,5) | 5 | 0.2 |
| [6,10) | 15 | m |
| [11,15) | n | P |
| [16,20) | 1 | 0.04 |
| 合计 | a | 1 |
(2)军干所决定对捐赠抗战纪念品的老干部进行表彰,对捐赠抗战纪念品数在[16,20]区间的老干部发放价值400元的奖品,对捐赠抗战纪念品数在[11,15]区间的老干部发放价值300元的奖品,对捐赠抗战纪念品数在[6,10]区间的老干部发放价值200元的奖品,对捐赠抗战纪念品数在[1,5]区间的老干部发放价100元的奖品,在所取样本中,任意抽取2人,并设x为此二人所获得奖品价值之差的绝对值,求x的分布列与数学期望E(X).
3.若两平行直线2x+y-4=0与y=-2x-m-2间的距离不大于$\sqrt{5}$,则m的取值范围是( )
| A. | [-11,-1] | B. | [-11,0] | C. | [-11,-6]∪(-6,-1] | D. | [-1,+∞) |
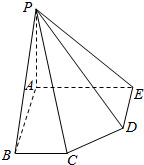 如图所示在五棱锥P-ABCDE中,侧棱PA⊥底面ABCDE,∠EAB=∠ABC=∠DEA=90°,AB=AE=2,BC=DE=1.求证:BD⊥平面PAC.
如图所示在五棱锥P-ABCDE中,侧棱PA⊥底面ABCDE,∠EAB=∠ABC=∠DEA=90°,AB=AE=2,BC=DE=1.求证:BD⊥平面PAC.