题目内容
求函数y=
的值域．
| 2x2-2x+3 |
| x2-x+1 |
考点：函数的值域
专题：函数思想,函数的性质及应用
分析：分母分子是齐次的，常用分离常数法，分母是二次的，用配方法即可可出值域．
解答：
解：y=
=2+
=2+
，
∵(x-
)2+
∈[
，+∞)，
∴y∈（2，
]，即函数的值域为（2，
]．
| 2(x2-x+1)+1 |
| x2-x+1 |
| 1 |
| x2-x+1 |
| 1 | ||||
(x-
|
∵(x-
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
∴y∈（2，
| 10 |
| 3 |
| 10 |
| 3 |
点评：分离常数法是求函数值域的常用方法之一，属于基础题．
练习册系列答案
相关题目
过曲线y=
x3上的点P的切线l的方程为12x-3y=16，那么P点坐标可能为（ ）
| 1 |
| 3 |
A、（1，-
| ||
B、（2，
| ||
C、（-1，-
| ||
D、（3，
|
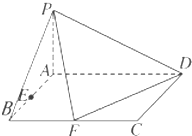已知四棱锥P-ABCD的底面ABCD是矩形，PA⊥平面ABCD，AD=2，AB=1，E，F分别是线段AB，BC的中点，
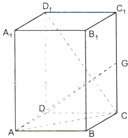如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，G是CC1上的动点．
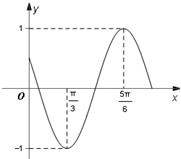已知函数f（x）=cos（ωx+φ）（ω＞0，0＜φ＜