题目内容
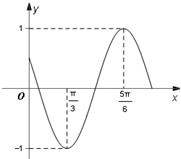已知函数f（x）=cos（ωx+φ）（ω＞0，0＜φ＜| π |
| 2 |
（1）求函数解析式；
（2）若方程f（x）=m在[-
| π |
| 12 |
| 13π |
| 12 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：（1）根据已知中函数的图象求出函数的周期，要求出ω，进而根据“第一点向左平移量”法可求出φ值，代入可得函数的解析式；
（2）分析函数在[-
，
]图象和性质，进而得到方程f（x）=m在[-
，
]有两个不同的实根，即函数y=f（x）和y=m的图象在[-
，
]有两个不同的交点时，m的取值范围．
（2）分析函数在[-
| π |
| 12 |
| 13π |
| 12 |
| π |
| 12 |
| 13π |
| 12 |
| π |
| 12 |
| 13π |
| 12 |
解答：
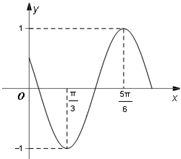解：（1）∵
=
-
=
，
故T=π，
又∵ω＞0，
故ω=2，
故函数图象第一点的坐标为（-
，0）点，
即向左平移量L=
，
故φ=ω•L=
，
故f(x)=cos(2x+
)…（4分）
（2）由（1）中函数解析式可得当x∈[-
，
]或x∈[
，
]时，函数为减函数，
当x∈[
，
]时，函数为减函数，
又∵f（-
）=cos
=
，f（
）=cos
=0，
故当m∈(-1，0)∪(
，1)时，函数y=f（x）和y=m的图象在[-
，
]有两个不同的交点
即方程f（x）=m有两个不同的实根，
故m的取值范围为(-1，0)∪(
，1)…（8分）
解：（1）∵| T |
| 2 |
| 5π |
| 6 |
| π |
| 3 |
| π |
| 2 |
故T=π，
又∵ω＞0，
故ω=2，
故函数图象第一点的坐标为（-
| π |
| 6 |
即向左平移量L=
| π |
| 6 |
故φ=ω•L=
| π |
| 3 |
故f(x)=cos(2x+
| π |
| 3 |
（2）由（1）中函数解析式可得当x∈[-
| π |
| 12 |
| π |
| 3 |
| 5π |
| 6 |
| 13π |
| 12 |
当x∈[
| π |
| 3 |
| 5π |
| 6 |
又∵f（-
| π |
| 12 |
| π |
| 6 |
| ||
| 2 |
| 13π |
| 12 |
| 5π |
| 2 |
故当m∈(-1，0)∪(
| ||
| 2 |
| π |
| 12 |
| 13π |
| 12 |
即方程f（x）=m有两个不同的实根，
故m的取值范围为(-1，0)∪(
| ||
| 2 |
点评：本题考查的知识点是正弦型函数的图象和性质，其中根据已知求出函数的解析式是解答的关键．
练习册系列答案
相关题目
已知集合A={-1，0，1}，B={y|y=sinπx，x∈A}，则A∩B=（ ）
| A、{-1} | B、{0} |
| C、{1} | D、∅ |
