题目内容
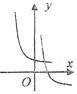
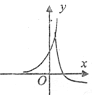
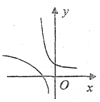
3．已知函数f（x）=（$\frac{1}{e}$）x+lnx，正数a，b，c满足a＜b＜c，且f（a）•f（b）•f（c）＞0，若实数x0是方程f（x）=0的一个解，那么下列不等式中不可能成立的是（ ）| A． | x0＞c | B． | x0＞b | C． | x0＜c | D． | x0＜a |
分析 先对函数f（x）=e-x+lnx进行求导，判定在定义域上的单调性，根据单调性即可比较．
解答 解：f’（x）=-e-x+$\frac{1}{x}$=$\frac{1-\frac{x}{{e}^{x}}}{x}$，
∵x＞0，$\frac{x}{{e}^{x}}$＜1
∴f’（x）＞0则函数f（x）在（0，+∞）上单调递增函数
∵正数a，b，c满足a＜b＜c，且f（a）•f（b）•f（c）＞0，
∴f（a）＜0，f（b）＜0，f（c）＞0，或f（a）＞0，f（b）＞0，f（c）＞0，
若实数x0是方程f（x）=0的一个解，
则a＜b＜x0＜c，或x0＜a＜b＜c，
故选：A．
点评 本题主要考查了函数与方程的综合运用，以及函数的单调性的应用，属于中档题．
练习册系列答案
相关题目
6．函数f（x）=3sin（2x-$\frac{π}{3}$）的图象可以由y=3sin2x的图象（ ）
| A． | 向右平移$\frac{π}{3}$个单位长度得到 | B． | 向左平移$\frac{π}{3}$个单位长度得到 | ||
| C． | 向右平移$\frac{π}{6}$个单位长度得到 | D． | 向左平移$\frac{π}{6}$个单位长度得到 |
3．下面四个命题中的真命题是（ ）
| A． | 命题“?x≥2，均有x2-3x+2≥0”的否定是：“?x＜2，使得x2-3x+2＜0” | |
| B． | 命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1” | |
| C． | 采用系统抽样法从某班按学号抽取5名同学参加活动，学号为5、16、27、38、49的同学均被选出，则该班人数可能为60 | |
| D． | 在某项测量中，测量结果X服从正态分布N（1，σ2）（σ＞0），若X在（0，1）内取值的概率为0.3，则X在（0，2）内取值的概率为0.6 |
10．
私家车的尾气排放是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成如表：
（Ⅰ）完成被调查人员的频率分布直方图；
（Ⅱ）若从年龄在[55，65），的被调查者中各随机选取2人进行追踪调查，记选中的2人中赞成“车辆限行”的人数为X，求随机变量X的分布列和数学期望．
私家车的尾气排放是造成雾霾天气的重要因素之一，因此在生活中我们应该提倡低碳生活，少开私家车，尽量选择绿色出行方式，为预防雾霾出一份力．为此，很多城市实施了机动车尾号限行，我市某报社为了解市区公众对“车辆限行”的态度，随机抽查了50人，将调查情况进行整理后制成如表：| 年龄（岁） | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
（Ⅱ）若从年龄在[55，65），的被调查者中各随机选取2人进行追踪调查，记选中的2人中赞成“车辆限行”的人数为X，求随机变量X的分布列和数学期望．
15．已知函数f（x）的导函数f′（x）的图象如图所示，那么下面说法正确的是（ ）
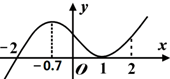
| A． | y=f（x）在（-∞，-0.7）上单调递增 | B． | y=f（x）在（-2，2）上单调递增 | ||
| C． | 在x=1时，函数y=f（x）取得极值 | D． | y=f（x）在x=0处切线的斜率小于零． |
