题目内容
5.在平面直角坐标系xOy中,以坐标原点为极轴,x轴正半轴为极轴建立极坐标系,已知曲线C的极坐标方程为:ρ=$\frac{4cosθ}{si{n}^{2}θ}$,直线l的参数方程是$\left\{\begin{array}{l}{x=2+tcosα}\\{y=2+tsinα}\end{array}\right.$(t为参数,0≤α<π).(1)求曲线C的直角坐标方程;
(2)设直线l与曲线C交于两点A,B,且线段AB的中点为M(2,2),求α.
分析 (1)利用极坐标方程与直角坐标方程的转化方法,求曲线C的直角坐标方程;
(2)利用点差法,即可得出结论.
解答 解:(1)曲线C的极坐标方程为:ρ=$\frac{4cosθ}{si{n}^{2}θ}$,直角坐标方程为y2=4x;
(2)直线l的参数方程是$\left\{\begin{array}{l}{x=2+tcosα}\\{y=2+tsinα}\end{array}\right.$(t为参数,0≤α<π),普通方程为y-2=tanα(x-2),
设A(x1,y1),B(x2,y2),代入抛物线方程,相减,可得tanα=1,∴α=45°.
点评 本题考查极坐标方程与直角坐标方程的转化,考查点差法的运用,比较基础.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
16.用半径为R的圆铁皮剪一个内接矩形,再以内接矩形的两边分别作为圆柱的高与底面半径,则圆柱的体积最大时,该圆铁皮面积与其内接矩形的面积比为( )
| A. | $\frac{3\sqrt{3}π}{8}$ | B. | $\frac{3\sqrt{3}π}{7}$ | C. | $\frac{3\sqrt{2}π}{8}$ | D. | $\frac{3\sqrt{2}π}{7}$ |
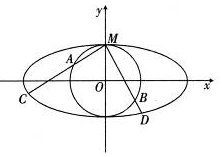 如图,圆O(O为坐标原点)与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于点M(0,1).
如图,圆O(O为坐标原点)与离心率为$\frac{{\sqrt{3}}}{2}$的椭圆T:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)相交于点M(0,1).