题目内容
12.已知|$\vec a$|=1,|$\vec b$|=$\sqrt{2}$,($\vec a$-$\vec b$)$⊥\overrightarrow a$,则$\vec a$与$\vec b$的夹角是$\frac{π}{4}$.分析 利用两个向量的数量积的定义,求得$\vec a$与$\vec b$的夹角的余弦值,可得$\vec a$与$\vec b$的夹角.
解答 解:设$\vec a$与$\vec b$的夹角为θ,θ∈[0,π],则由已知|$\vec a$|=1,|$\vec b$|=$\sqrt{2}$,($\vec a$-$\vec b$)$⊥\overrightarrow a$,
可得($\vec a$-$\vec b$)•$\overrightarrow{a}$=${\overrightarrow{a}}^{2}$-$\overrightarrow{a}•\overrightarrow{b}$=1-1•$\sqrt{2}$•cosθ=0,∴cosθ=$\frac{\sqrt{2}}{2}$,∴θ=$\frac{π}{4}$,
故答案为:$\frac{π}{4}$.
点评 本题主要考查两个向量的数量积的定义,属于基础题.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
3.已知函数f(x)=($\frac{1}{e}$)x+lnx,正数a,b,c满足a<b<c,且f(a)•f(b)•f(c)>0,若实数x0是方程f(x)=0的一个解,那么下列不等式中不可能成立的是( )
| A. | x0>c | B. | x0>b | C. | x0<c | D. | x0<a |
20.设α为△ABC的内角,且tanα=-$\frac{3}{4}$,则cos2α的值为( )
| A. | $\frac{7}{25}$ | B. | -$\frac{24}{25}$ | C. | -$\frac{1}{25}$ | D. | $\frac{1}{25}$ |
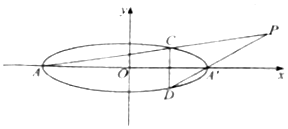 如图所示,椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左,右顶点分别为A,A′,线段CD是垂直于椭圆长轴的弦,连接AC,DA′相交于点P,则点P的轨迹方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1.
如图所示,椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左,右顶点分别为A,A′,线段CD是垂直于椭圆长轴的弦,连接AC,DA′相交于点P,则点P的轨迹方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1.