题目内容
10. 私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成如表:
私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成如表:| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(Ⅱ)若从年龄在[55,65),的被调查者中各随机选取2人进行追踪调查,记选中的2人中赞成“车辆限行”的人数为X,求随机变量X的分布列和数学期望.
分析 (Ⅰ)由已知得各组的频率分别是:0.1,0.2,0.3,0.2,0.1,0.1,分别除以10可得图中各组的纵坐标,由此能作出被调查人员的频率分布直方图,如图.
(Ⅱ)由表知年龄在[55,65)内的有5人,不赞成的有2人,因此X=0,1,2.根据P(X=k)=$\frac{{∁}_{3}^{k}{∁}_{2}^{2-k}}{{∁}_{5}^{2}}$即可得出.
解答 解:(Ⅰ)由已知得各组的频率分别是:
0.1,0.2,0.3,0.2,0.1,0.1,
∴图中各组的纵坐标分别是:
0.01,0.02,0.03,0.02,0.01,0.01,
由此能作出被调查人员的频率分布直方图,如右图:
(Ⅱ)由表知年龄在[55,65)内的有5人,
不赞成的有2人,因此X=0,1,2.
则P(X=k)=$\frac{{∁}_{3}^{k}{∁}_{2}^{2-k}}{{∁}_{5}^{2}}$,可得P(X=0)=$\frac{1}{10}$,P(X=1)=$\frac{6}{10}$,P(X=0)=$\frac{3}{10}$.
可得X的分布列:
| X | 0 | 1 | 2 |
| P | $\frac{1}{10}$ | $\frac{6}{10}$ | $\frac{3}{10}$ |
点评 本题考查了频率分布直方图的性质、超几何分布列及其数学期望,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.若集合A={x|1≤2x≤8},B={x|(x-2)(x+1)>0},则A∩B=( )
| A. | (2,3] | B. | [2,3] | C. | (-∞,0)∪(0,2] | D. | (-∞,-1)∪(0,3] |
5.在平行四边形ABCD中,AD=1,∠BAD=30°,E为CD的中点.若$\overrightarrow{AC}•\overrightarrow{BE}=1$,则AB的长为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
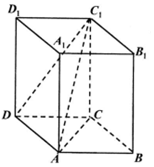 如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.
如图,棱柱ABCD-A1B1C1D1中,底面ABCD是平行四边形,侧棱AA1⊥底面ABCD,AB=1,AC=$\sqrt{3}$,BC=BB1=2.