题目内容

13．函数y=2-x与$y=-{log_{\frac{1}{2}}}（{-x}）$图象的大致形状是（　　）
A．B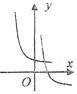．C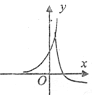．D．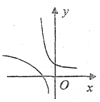

分析 确定函数过定点，函数的单调性，即可得出结论．

解答 解：函数y=2-x过（0，1），单调递减，$y=-{log_{\frac{1}{2}}}（{-x}）$过（-1，0），在（-∞，0）单调递减，
故选D．

点评 本题考查函数的图象，考查数形结合的数学思想，比较基础．

练习册系列答案
相关题目
3．已知函数f（x）=（$\frac{1}{e}$）x+lnx，正数a，b，c满足a＜b＜c，且f（a）•f（b）•f（c）＞0，若实数x0是方程f（x）=0的一个解，那么下列不等式中不可能成立的是（　　）
A．x0＞cB．x0＞bC．x0＜cD．x0＜a
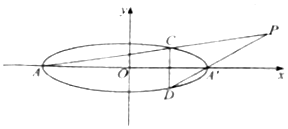4．如图所示，椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左，右顶点分别为A，A′，线段CD是垂直于椭圆长轴的弦，连接AC，DA′相交于点P，则点P的轨迹方程为$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{4}$=1．
1．已知两点F1（-4，0），F2（4，0），到它们的距离的和是10的点M的轨迹方程是$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1．
8．读下的程序，并回答问题．

该程序的作用是输入x的值，输出y的值．
（1）画出该程序对应的程序框图．
（2）若要使输入的x值与输出的y值相等，这样的x值有几个？
18．函数$y={log_{\frac{1}{2}}}（{-{x^2}+2x+1}）$（x∈[0，$\sqrt{2}$]）的值域是-[-1，0]．
5．已知抛物线的方程为y2=2mx（m＞0），焦点坐标为（1，0），则m等于（　　）
A．4B．3C．2D．1
2．已知$\sqrt{2+\frac{2}{3}}=2\sqrt{\frac{2}{3}}$，$\sqrt{3+\frac{3}{8}}=3\sqrt{\frac{3}{8}}$，$\sqrt{8+\frac{b}{a}}=8\sqrt{\frac{b}{a}}$，则a、b的值分别是63，8．
3．若x，y满足$\left\{{\begin{array}{l}{x-y≥0}\\{x+y≤1}\\{y≥0}\end{array}}\right.$，则z=x+2y的最大值为2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网