题目内容
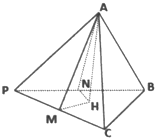在三棱锥P-ABC中，PA=a，PB=b，PC=c，且∠BPC=α，∠APC=β，∠APB=γ．（1）A到面PBC的距离；
（2）四面体P-ABC的体积．
考点：棱柱、棱锥、棱台的体积,点、线、面间的距离计算
专题：计算题,空间位置关系与距离
分析：（1）作AH⊥平面ABC，垂足为H，作HN⊥PB，HM⊥PC，连接AN，AM，则AN⊥PB．AM⊥PC，求出PM，PN，MN，可得PH，即可求出A到面PBC的距离；
（2）利用三棱锥的体积公式，可求四面体P-ABC的体积．
（2）利用三棱锥的体积公式，可求四面体P-ABC的体积．
解答：
解：（1）作AH⊥平面ABC，垂足为H，作HN⊥PB，HM⊥PC，连接AN，AM，则AN⊥PB．AM⊥PC，
∵PA=a，∠APC=β，∠APB=γ．
∴PM=acosβ，PN=acosγ，
∴MN=
，
∴PH=
，
∴AH=
；
（2）四面体P-ABC的体积=
×
bcsinα×
=
abc
．
∵PA=a，∠APC=β，∠APB=γ．
∴PM=acosβ，PN=acosγ，
∴MN=
| a2cos2β+a2cos2γ-2a2cosαcosβcosγ |
∴PH=
| 1 |
| sinα |
| a2cos2β+a2cos2γ-2a2cosαcosβcosγ |
∴AH=
| a |
| sinα |
| sin2α-cos2β-cos2γ+2cosαcosβcosγ |
（2）四面体P-ABC的体积=
| 1 |
| 3 |
| 1 |
| 2 |
| a |
| sinα |
| sin2α-cos2β-cos2γ+2cosαcosβcosγ |
=
| 1 |
| 6 |
| sin2α-cos2β-cos2γ+2cosαcosβcosγ |
点评：本题考查三棱锥的体积，考查A到面PBC的距离的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
已知
，
为单位向量，且满足（2
+
）•
=0，则＜
，
＞=（ ）
| e1 |
| e2 |
| e1 |
| e2 |
| e2 |
| e1 |
| e2 |
| A、30° | B、60° |
| C、120° | D、150° |
点F为双曲线
-
=1（a＞0，b＞0）的左焦点，过F的直线l交双曲线右支于点E，若圆x2+y2=
上一点P满足
+
=2
，且∠FOP为锐角，则该双曲线的离心率的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
| OF |
| OE |
| OP |
A、（
| ||||||
B、（
| ||||||
C、（
| ||||||
D、（
|
设α、β∈[-
，
]，且满足sinαcosβ+sinβcosα=1，则sinα+sinβ的取值范围是（ ）
| π |
| 2 |
| π |
| 2 |
A、[-
| ||||
B、[-1，
| ||||
C、[0，
| ||||
D、[1，
|
