题目内容
点F为双曲线
-
=1(a>0,b>0)的左焦点,过F的直线l交双曲线右支于点E,若圆x2+y2=
上一点P满足
+
=2
,且∠FOP为锐角,则该双曲线的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| 4 |
| OF |
| OE |
| OP |
A、(
| ||||||
B、(
| ||||||
C、(
| ||||||
D、(
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:确定P是EF的中点,再结合余弦定理,可得结论.
解答:
解:设右焦点为F′,
∵
+
=2
,∴P是EF的中点,
∴EF′=2OP=a,
∴EF=3a,
∵∠FOP为锐角,
∴∠FEF′为钝角,
∴(3a)2+a2>4c2,
∴e<
,
故选:B.
∵
| OF |
| OE |
| OP |
∴EF′=2OP=a,
∴EF=3a,
∵∠FOP为锐角,
∴∠FEF′为钝角,
∴(3a)2+a2>4c2,
∴e<
| ||
| 2 |
故选:B.
点评:本题主要考查双曲线的标准方程,以及双曲线的简单性质的应用,属于中档题.

练习册系列答案
相关题目
四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…这样交替进行下去,那么第2014次互换座位后,小兔坐在第( )号座位上.
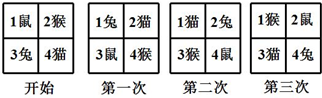

| A、1 | B、2 | C、3 | D、4 |
若函数f(x)=xlnx-a有两个零点,则实数a的取值范围为( )
A、[0,
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(-
|
已知正三角形ABC的边长是3,D是BC上的点,BD=1,则
•
=( )
| AD |
| BC |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
曲线
+
=1与
+
=1(k<9)有相同的( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、长轴 | B、准线 | C、焦点 | D、离心率 |
若θ为三角形一个内角,且对任意实数x,x2cosθ-4xsinθ+6>0恒成立,则θ的取值范围为( )
A、(
| ||||
B、(0,
| ||||
C、(0,
| ||||
D、(
|
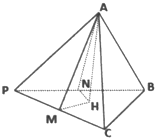 在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.
在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.