题目内容
求函数y=
的值域.
| 3-x |
| 2x-1 |
考点:函数的值域
专题:函数的性质及应用
分析:对函数的解析式化简成y=-
(1-
)的形式,根据函数的性质求得函数y的范围.
| 1 |
| 2 |
| ||
x-
|
解答:
解:y=-
•
=-
(1-
),
∵
≠0,
∴y≠-
,
即函数的值域为(-∞,-
)∪(-
,+∞).
| 1 |
| 2 |
| x-3 | ||
x-
|
| 1 |
| 2 |
| ||
x-
|
∵
| ||
x-
|
∴y≠-
| 1 |
| 2 |
即函数的值域为(-∞,-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了函数的值域问题.本题也可以y表示出x,利用反函数法求得值域.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
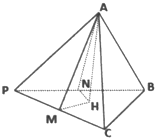 在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.
在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.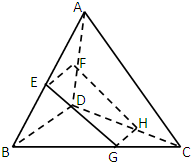 如图,已知空间四边形ABCD,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且
如图,已知空间四边形ABCD,E,F分别是AB,AD的中点,G,H分别是BC,CD上的点,且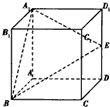 如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.