题目内容
AB是底部B是一个不可到达的建筑物，A为建筑物的最高点，设计一个方案测量AB的高度．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：构造三角形，利用在H、G两点用测角仪器测得A的仰角，即可得出方案测量AB的高度．
解答：
解：AB底部是不可到达的建筑物，在地平面上，选C，D两点，CD=a，从C，D两点看建筑物的顶部A的仰角分别是α，β，可用α，β，a表示AB的高度．
在△ACD中，由正弦定理可得AC=
在△ACB中，AB=ACsinα=
．
在△ACD中，由正弦定理可得AC=
| asinβ |
| sin(α-β) |
在△ACB中，AB=ACsinα=
| asinβsinα |
| sin(α-β) |
点评：本题主要考查了解三角形的实际应用，考查了学生分析问题和解决问题的能力．
练习册系列答案
相关题目
四个小动物换座位，开始是鼠、猴、兔、猫分别坐1、2、3、4号位上（如图），第一次前后排动物互换座位，第二次左右列动物互换座位，…这样交替进行下去，那么第2014次互换座位后，小兔坐在第（ ）号座位上．
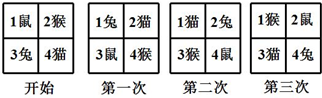
| A、1 | B、2 | C、3 | D、4 |
若θ为三角形一个内角，且对任意实数x，x2cosθ-4xsinθ+6＞0恒成立，则θ的取值范围为（ ）
A、（
| ||||
B、（0，
| ||||
C、（0，
| ||||
D、（
|
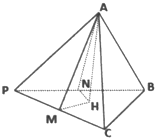在三棱锥P-ABC中，PA=a，PB=b，PC=c，且∠BPC=α，∠APC=β，∠APB=γ．
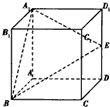如图所示，在正方体ABCD-A1B1C1D1中，E是棱DD1的中点．