题目内容
在调查男女乘客是否晕机的情况中,已知男乘客晕机为20人,不会晕机的为10人,而女乘客晕机为10人,不会晕机的为20人,
(1)根据以上数据建立一个2×2的列联表;
(2)试判断是否晕机与性别有关?参考公式:
(K2=
)
(1)根据以上数据建立一个2×2的列联表;
(2)试判断是否晕机与性别有关?参考公式:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)根据条件中所给的数据,写出列联表,注意各个部分的数据不要写错位置,做出合计要填在表中.
(2)根据列联表和求观测值的公式,把数据代入公式,求出观测值,把观测值同临界值进行比较,得到有90%的把握认为晕机与性别有关.
(2)根据列联表和求观测值的公式,把数据代入公式,求出观测值,把观测值同临界值进行比较,得到有90%的把握认为晕机与性别有关.
解答:
解:(1)2×2列联表如下:
(2)假设是否晕机与性别无关,则k2的观测值k2=
≈6.667>6.635
∴有90%的把握认为晕机与性别有关
| 晕机 | 不晕机 | 合计 | |
| 男乘客 | 20 | 10 | 30 |
| 女乘客 | 10 | 20 | 30 |
| 合计 | 30 | 30 | 60 |
| 60×(20×20-10×10)2 |
| 30×30×30×30 |
∴有90%的把握认为晕机与性别有关
点评:本题考查独立性检验,考查学生的计算能力,是一个基础题.

练习册系列答案
相关题目
已知双曲线C:
-
=1(b>0)的一条渐进线方程为y=
x,F1,F2分别为双曲线C的左右焦点,P为双曲线C上的一点,满足|PF1|:|PF2|=3:1,则|
+
|的值是( )
| x2 |
| 4 |
| y2 |
| b2 |
| ||
| 2 |
| PF1 |
| PF2 |
| A、4 | ||||
B、2
| ||||
C、2
| ||||
D、
|
曲线
+
=1与
+
=1(k<9)有相同的( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、长轴 | B、准线 | C、焦点 | D、离心率 |
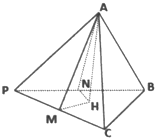 在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.
在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.