题目内容
圆C的参数方程为
(∂为参数),直线l的极坐标方程为ρsin(θ-
)=
(1)求圆与直线的直角坐标方程;
(2)直线l与圆C交于A、B,与x轴交于P,求PA+PB的值.
|
| π |
| 4 |
| 2 |
(1)求圆与直线的直角坐标方程;
(2)直线l与圆C交于A、B,与x轴交于P,求PA+PB的值.
考点:参数方程化成普通方程
专题:坐标系和参数方程
分析:(1)利用同角三角函数的平方关系可得圆的直角坐标方程,利用极坐标与直角坐标的互化公式可得直线l的直角坐标方程;
(2)利用直线参数方程的意义,把直线的参数方程代入圆的方程即可得出.
(2)利用直线参数方程的意义,把直线的参数方程代入圆的方程即可得出.
解答:
解:(1)由圆C的参数方程为
(∂为参数),可得(x-2)2+(y-3)2=cos2α+sin2α=1,
∴圆C的直角坐标方程为:(x-2)2+(y-3)2=1,
直线l的极坐标方程ρsin(θ-
)=
展开可得
(ρsinθ-ρcosθ)=
,化为y-x=2.
∴直线l的直角坐标方程为x-y+2=0;
(2)由直线l的直角坐标方程为x-y+2=0,令y=0,可得x=-2,∴P(-2,0).
设直线l的参数方程为
,
代入圆C的方程可得(-2+
t-2)2+(
t-3)2=1,
化为t2-7
t+24=0,
∴t1+t2=7
>0,t1t2>0.
即PA+PB=7
.
|
∴圆C的直角坐标方程为:(x-2)2+(y-3)2=1,
直线l的极坐标方程ρsin(θ-
| π |
| 4 |
| 2 |
| ||
| 2 |
| 2 |
∴直线l的直角坐标方程为x-y+2=0;
(2)由直线l的直角坐标方程为x-y+2=0,令y=0,可得x=-2,∴P(-2,0).
设直线l的参数方程为
|
代入圆C的方程可得(-2+
| ||
| 2 |
| ||
| 2 |
化为t2-7
| 2 |
∴t1+t2=7
| 2 |
即PA+PB=7
| 2 |
点评:本题考查了同角三角函数的平方关系、圆的方程、极坐标与直角坐标的互化公式、直线与圆的位置关系、直线参数方程的意义等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
若函数f(x)=xlnx-a有两个零点,则实数a的取值范围为( )
A、[0,
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(-
|
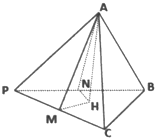 在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.
在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.