题目内容
已知
,
为单位向量,且满足(2
+
)•
=0,则<
,
>=( )
| e1 |
| e2 |
| e1 |
| e2 |
| e2 |
| e1 |
| e2 |
| A、30° | B、60° |
| C、120° | D、150° |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积运算和特殊角的三角函数即可得出.
解答:
解:∵
,
为单位向量,且满足(2
+
)•
=0,
∴2
•
+
2=0,
∴2cos<
,
>+1=0,
∴cos<
,
>=-
.
∴<
,
>=120°.
故选:C.
| e1 |
| e2 |
| e1 |
| e2 |
| e2 |
∴2
| e1 |
| e2 |
| e2 |
∴2cos<
| e1 |
| e2 |
∴cos<
| e1 |
| e2 |
| 1 |
| 2 |
∴<
| e1 |
| e2 |
故选:C.
点评:本题考查了数量积运算、特殊角的三角函数、向量的夹角,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
已知F1、F2是离心率为
的双曲线C的左、右焦点,点P在C上,若|PF1|=2|PF2|,则cos∠F1PF2=( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
-cosx,若
<a<b<
,则( )
| 1 |
| 2x |
| π |
| 3 |
| 5π |
| 6 |
| A、f(a)>f(b) |
| B、f(a)<f(b) |
| C、f(a)=f(b) |
| D、f(a)f(b)>0 |
已知双曲线C:
-
=1(b>0)的一条渐进线方程为y=
x,F1,F2分别为双曲线C的左右焦点,P为双曲线C上的一点,满足|PF1|:|PF2|=3:1,则|
+
|的值是( )
| x2 |
| 4 |
| y2 |
| b2 |
| ||
| 2 |
| PF1 |
| PF2 |
| A、4 | ||||
B、2
| ||||
C、2
| ||||
D、
|
四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…这样交替进行下去,那么第2014次互换座位后,小兔坐在第( )号座位上.
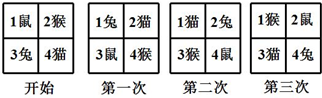

| A、1 | B、2 | C、3 | D、4 |
若函数f(x)=xlnx-a有两个零点,则实数a的取值范围为( )
A、[0,
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(-
|
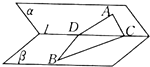 已知二面角α-l-β的大小为60°,A∈α,B∈β,AC⊥l于C,BD⊥l于D,AC=BD=4,CD=3,则AD与BC所成角的余弦值为
已知二面角α-l-β的大小为60°,A∈α,B∈β,AC⊥l于C,BD⊥l于D,AC=BD=4,CD=3,则AD与BC所成角的余弦值为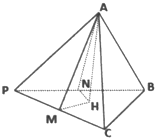 在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.
在三棱锥P-ABC中,PA=a,PB=b,PC=c,且∠BPC=α,∠APC=β,∠APB=γ.