题目内容
现有甲、乙、丙三人参加某电视台的应聘节目《非你莫属》,若甲应聘成功的概率为
,乙、丙应聘成功的概率均为
(0<t<2),且三个人是否应聘成功是相互独立的.
(Ⅰ)若乙、丙有且只有一个人应聘成功的概率等于甲应聘成功是相互独立的,求t的值;
(Ⅱ)记应聘成功的人数为ξ,若当且仅当ξ为2时概率最大,求E(ξ)的取值范围.
| 1 |
| 2 |
| t |
| 2 |
(Ⅰ)若乙、丙有且只有一个人应聘成功的概率等于甲应聘成功是相互独立的,求t的值;
(Ⅱ)记应聘成功的人数为ξ,若当且仅当ξ为2时概率最大,求E(ξ)的取值范围.
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:应用题,概率与统计
分析:(Ⅰ)根据乙、丙有且只有一个人应聘成功的概率等于甲应聘成功是相互独立的,建立方程,即可求t的值;
(Ⅱ)ξ的所有可能取值为0,1,2,3,求出相应的概率,即可得到ξ的分布列和期望,利用当且仅当ξ为2时概率最大,即可求E(ξ)的取值范围.
(Ⅱ)ξ的所有可能取值为0,1,2,3,求出相应的概率,即可得到ξ的分布列和期望,利用当且仅当ξ为2时概率最大,即可求E(ξ)的取值范围.
解答:
解:(Ⅰ)由题意得2×
×(1-
)=
,解得t=1.…(3分)
(Ⅱ)ξ的所有可能取值为0,1,2,3,
P(ξ=0)=(1-
)(1-
)(1-
)=
;P(ξ=1)=
×(1-
)×(1-
)+2×(1-
)×
×(1-
)=
;P(ξ=2)=2×
×
×(1-
)+(1-
)×
×
=
;
P(ξ=3)=
×
×
=
.
故ξ的分布列为:
…(7分)∴Eξ=t+
.…(8分)
由题意得:P(ξ=2)-P(ξ=1)=
>0,P(ξ=2)-P(ξ=0)=
>0,P(ξ=2)-P(ξ=3)=
>0,
又因为0<t<2
所以解得t的取值范围是1<t<2.…(11分)
所以
<Eξ<
.…(12分)
| t |
| 2 |
| t |
| 2 |
| 1 |
| 2 |
(Ⅱ)ξ的所有可能取值为0,1,2,3,
P(ξ=0)=(1-
| 1 |
| 2 |
| t |
| 2 |
| t |
| 2 |
| (2-t)2 |
| 8 |
| 1 |
| 2 |
| t |
| 2 |
| t |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
| t |
| 2 |
| 4-t2 |
| 8 |
| 1 |
| 2 |
| t |
| 2 |
| t |
| 2 |
| 1 |
| 2 |
| t |
| 2 |
| t |
| 2 |
| 4t-t2 |
| 8 |
P(ξ=3)=
| 1 |
| 2 |
| t |
| 2 |
| t |
| 2 |
| t2 |
| 8 |
故ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 2 |
由题意得:P(ξ=2)-P(ξ=1)=
| t-1 |
| 2 |
| -t2+4t-2 |
| 4 |
| 2t-t2 |
| 4 |
又因为0<t<2
所以解得t的取值范围是1<t<2.…(11分)
所以
| 3 |
| 2 |
| 5 |
| 2 |
点评:本题考查互斥事件的概率公式,考查离散型随机变量的分布列与期望,确定变量的取值,求出概率是关键.

练习册系列答案
相关题目
下列各式中值等于
的是( )
| 1 |
| 2 |
| A、sin15°cos15° | ||||||
B、
| ||||||
C、cos2
| ||||||
D、
|
已知i为虚数单位,若
是纯虚数,则实数a的值为( )
| a+i |
| 1-i |
A、-
| ||
| B、-1 | ||
| C、1 | ||
D、
|
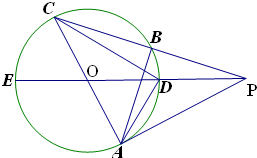 如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.
如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD. 在线路中,各原件能否正常工作是相互独立的,已知原件a,b,c,d,e能正常工作的概率是0.9,0.95,0.7,0.8,0.85,求线路畅通的概率.
在线路中,各原件能否正常工作是相互独立的,已知原件a,b,c,d,e能正常工作的概率是0.9,0.95,0.7,0.8,0.85,求线路畅通的概率.