题目内容
已知椭圆C:
+y2=1,点M1,M2…,M5为其长轴AB的6等分点,分别过这五点作斜率为k(k≠0)的一组平行线,交椭圆C于P1,P2,…,P10,则直线AP1,AP2,…,AP10这10条直线的斜率乘积为( )
| x2 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、-
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:利用椭圆的性质可得kAP1•kBP1=kAP2•kBP10=-
=-
.及其椭圆的对称性可得kBP1=kAP10,kBP10=kAP1,进而得出答案.
| b2 |
| a2 |
| 1 |
| 2 |
解答:
解:如图所示,
由椭圆的性质可得kAP1•kBP1=kAP2•kBP10=-
=-
.
由椭圆的对称性可得kBP1=kAP10,kBP10=kAP1,
∴kAP1•kAP10=-
,
同理可得kAP3•kAP8=kAP5•kAP6=kAP7•kAP4=kAP9•kAP2=-
.
∴直线AP1,AP2,…,AP10这10条直线的斜率乘积=(-
)5=-
.
故选:B.

由椭圆的性质可得kAP1•kBP1=kAP2•kBP10=-
| b2 |
| a2 |
| 1 |
| 2 |
由椭圆的对称性可得kBP1=kAP10,kBP10=kAP1,
∴kAP1•kAP10=-
| 1 |
| 2 |
同理可得kAP3•kAP8=kAP5•kAP6=kAP7•kAP4=kAP9•kAP2=-
| 1 |
| 2 |
∴直线AP1,AP2,…,AP10这10条直线的斜率乘积=(-
| 1 |
| 2 |
| 1 |
| 32 |
故选:B.
点评:本题考查了椭圆的性质可得kAP1•kBP1=-
及椭圆的对称性,考查了推理能力和计算能力,属于难题.
| b2 |
| a2 |

练习册系列答案
相关题目
方程1-z4=0在复数范围内的根共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知数列{an}满足an+1=an-2(n∈N+),它的前n项和为Sn,“a1=6”则是“Sn的最大值是S3”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知i为虚数单位,若
是纯虚数,则实数a的值为( )
| a+i |
| 1-i |
A、-
| ||
| B、-1 | ||
| C、1 | ||
D、
|
sin61°cos31°-cos61°sin31°=( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
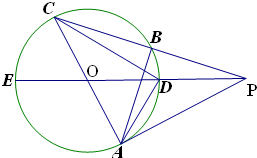 如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.
如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.