题目内容

4．安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，则不同的安排方式共有（　　）
A．12种B．18种C．24种D．36种

分析 把工作分成3组，然后安排工作方式即可．

解答 解：4项工作分成3组，可得：${C}_{4}^{2}$=6，
安排3名志愿者完成4项工作，每人至少完成1项，每项工作由1人完成，
可得：6×${A}_{3}^{3}$=36种．
故选：D．

点评 本题考查排列组合的实际应用，注意分组方法以及排列方法的区别，考查计算能力．

练习册系列答案
相关题目
14．在直角坐标系xOy中，直线l1的参数方程为$\left\{\begin{array}{l}{x=2+t}\\{y=kt}\end{array}\right.$，（t为参数），直线l2的参数方程为$\left\{\begin{array}{l}{x=-2+m}\\{y=\frac{m}{k}}\end{array}\right.$，（m为参数）．设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．
（1）写出C的普通方程；
（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ（cosθ+sinθ）-$\sqrt{2}$=0，M为l3与C的交点，求M的极径．
15．已知x≥0，y≥0，且x+y=1，则x2+y2的取值范围是[$\frac{1}{2}$，1]．
12．某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为（　　）
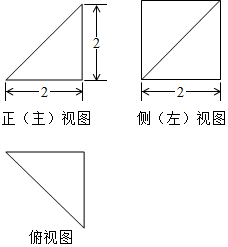
A．3$\sqrt{2}$B．2$\sqrt{3}$C．2$\sqrt{2}$D．2
19．已知抛物线C：y2=2px过点P（1，1）．过点（0，$\frac{1}{2}$）作直线l与抛物线C交于不同的两点M，N，过点M作x轴的垂线分别与直线OP、ON交于点A，B，其中O为原点．
（1）求抛物线C的方程，并求其焦点坐标和准线方程；
（2）求证：A为线段BM的中点．
9．函数f（x）=sin2x+$\sqrt{3}$cosx-$\frac{3}{4}$（x∈[0，$\frac{π}{2}$]）的最大值是1．
16．甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（　　）
A．乙可以知道四人的成绩B．丁可以知道四人的成绩
C．乙、丁可以知道对方的成绩D．乙、丁可以知道自己的成绩
17．若函数$f（x）=\sqrt{{2^x}-a}$的值域为[0，+∞），则a的取值范围是（0，+∞）．
18．已知当x∈[0，1]时，函数y=（mx-1）2 的图象与y=$\sqrt{x}$+m的图象有且只有一个交点，则正实数m的取值范围是（　　）
A．（0，1]∪[2$\sqrt{3}$，+∞）B．（0，1]∪[3，+∞）C．（0，$\sqrt{2}$）∪[2$\sqrt{3}$，+∞）D．（0，$\sqrt{2}$]∪[3，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网