题目内容
9.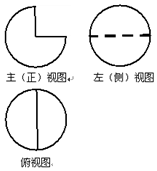 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中俯视图与左视图均为半径是1的圆,则这个几何体的体积是( )| A. | $\frac{4π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | π |
分析 由三视图知该几何体是一个球体截去$\frac{1}{4}$剩下的几何体,由题意求出球的半径,由球体的体积公式求出几何体的体积.
解答 解:由三视图知几何体是:
一个球体截去$\frac{1}{4}$剩下的几何体,且球的半径是1,
所以几何体的体积V=$\frac{3}{4}×\frac{4}{3}×π×{1}^{3}$=π,
故选D.
点评 本题考查了由三视图求几何体的体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
14.设$a={3^{0.2}},b={log_π}3,c={log_3}cos\frac{{\sqrt{2}}}{4}π$,则a,b,c关系正确的是( )
| A. | b>a>c | B. | a>b>c | C. | b>c>a | D. | c>b>a |
1.设 $a=ln\frac{1}{2},b={2^{\frac{1}{e}}},c={e^{-2}}$,则( )
| A. | c<b<a | B. | c<a<b | C. | a<c<b | D. | a<b<c |
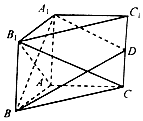 如图所示,三棱柱A1B1C1-ABC的侧棱AA1⊥底面ABC,AB⊥AC,AB=AA1,D是棱CC1的中点.
如图所示,三棱柱A1B1C1-ABC的侧棱AA1⊥底面ABC,AB⊥AC,AB=AA1,D是棱CC1的中点.