题目内容
5.若命题:“$?{x_0}∈R,a{x^2}-ax-2>0$”为假命题,则a的取值范围是( )| A. | (-∞,-8]∪[0,+∞) | B. | (-8,0) | C. | (-∞,0] | D. | [-8,0] |
分析 原命题若为假命题,则其否定必为真,即 ax2-ax-2≤0恒成立,由二次函数的图象和性质,解不等式可得答案.
解答 解:∵命题$?{x_0}∈R,a{x^2}-ax-2>0$”为假命题,命题“?x∈R,ax2-ax-2≤0”为真命题,
当a=0时,-2≤0成立,
当a≠0时,a<0,故方程ax2-ax-2=0的△=a2+8a≤0解得:-8≤a<0,
故a的取值范围是:[-8,0]
故选:D
点评 本题的知识点命题真假的判断与应用,其中将问题转化为恒成立问题,是解答本题的关键.

练习册系列答案
相关题目
13.已知非零实数a,b满足a<b,则下列不等式中一定成立的是( )
| A. | a+b>0 | B. | $\frac{1}{a}>\frac{1}{b}$ | C. | ab<b2 | D. | a3-b3<0 |
14.设$a={3^{0.2}},b={log_π}3,c={log_3}cos\frac{{\sqrt{2}}}{4}π$,则a,b,c关系正确的是( )
| A. | b>a>c | B. | a>b>c | C. | b>c>a | D. | c>b>a |
15.在△ABC中,“A<30°”是“$sinA<\frac{1}{2}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
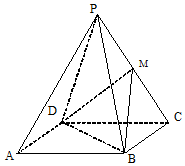 已知四棱锥P-ABCD中底面四边形ABCD是正方形,各侧面都是边长为2的正三角形,M是棱PC的中点.建立空间直角坐标系,利用空间向量方法解答以下问题:
已知四棱锥P-ABCD中底面四边形ABCD是正方形,各侧面都是边长为2的正三角形,M是棱PC的中点.建立空间直角坐标系,利用空间向量方法解答以下问题: