题目内容

1．已知箱内有质量和大小相同的20个红球，80个黑球，规定从中任意取出1个，记录它的颜色后再放回箱内，搅拌均匀后再任意取出1个，记录它的颜色后又放回箱内搅拌均匀，从此连续抽取三次．试求：
（1）事件A：“第一次取出黑球，第二次取出红球，第三次取出黑球”的概率；
（2）如果有50人分别依次进行这样（每人按规则均取球三次）的抽取，试推测约有多少人取出2个黑球，1个红球？

分析 （1）根据条件概率的公式计算即可；（2）根据（1）推测即可．

解答 解：（1）由题意得：
满足条件的概率是P=$\frac{{C}_{80}^{1}{•C}_{20}^{1}{•C}_{80}^{1}}{{100}^{3}}$=$\frac{16}{125}$，；
（2）由题意得：$\frac{16}{125}$×50≈6，
故推测约有6人取出2个黑球，1个红球．

点评 本题考查了古典概型问题，考查条件概率，是一道基础题．

练习册系列答案
相关题目
11．已知a，b，c为圆O上的三点，若$\overrightarrow{OA}=\frac{1}{2}（\overrightarrow{AB}+\overrightarrow{AC}）$，|$\overrightarrow{AB}$|=3，|$\overrightarrow{AC}$|=4，则|$\overrightarrow{AO}$|=$\frac{5}{2}$．
12．将边长分别为1、2、3、4、…、n、n+1、…（n∈N*）的正方形叠放在一起，形成如图所示的图形．由小到大，依次记各阴影部分所在的图形为第1个、第2个、…、第n个阴影部分图形．设前n个阴影部分图形的面积的平均值为f（n）．记数列{an}满足a1=1，an+1=$\left\{\begin{array}{l}f（n）\;\;当n为奇数\\ f（{a_n}）当n为偶数\end{array}$．
（1）求f（n）的表达式；
（2）写出a2、a3的值，并求数列{an}的通项公式．
（3）记$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc．若bn=an+s（s∈R），且$|\begin{array}{l}{{b}_{n}}&{{b}_{n+2}}\\{{b}_{n+1}}&{{b}_{n+1}}\end{array}|$＜0恒成立，求s的取值范围．
9．过三点A（1，3），B（4，2），C（1，-7）的圆M交于y轴于P、Q两点．
（1）求线段PQ的长；
（2）动圆N的半径为1，N在直线4x-3y+20=0上运动，判断圆M和圆N能否有公共点，并说明理由．
16．下列关于回归分析的说法正确的是④⑤（填上所有正确说法的序号）
①相关系数r越小，两个变量的相关程度越弱；
②残差平方和越大的模型，拟合效果越好；
③用相关指数R2来刻画回归效果时，R2越小，说明模型的拟合效果越好；
④用最小二乘法求回归直线方程，是寻求使$\sum_{i=1}^n{{{（{y_i}-b{x_i}-a）}^2}}$取最小值时的a，b的值；
⑤在残差图中，残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适，这样的带状区域的宽度越窄，模型拟合精度越高．
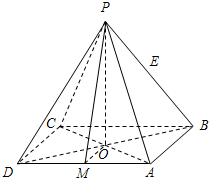6．如图所示，四棱锥P-ABCD中，PA=PB=PC=PD，AB=a，O为底面正方形的中心，侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$．
（1）求侧面PAD与底面ABCD所成的二面角的大小；
（2）若E是PB的中点，求异面直线PD与AE所成角的正切值．
13．已知f（x）=x3-$\frac{9}{2}$x2+6x-a，若对任意的x，f′（x）≥m恒成立，则m的最大值为（　　）
A．3B．2C．1D．-$\frac{3}{4}$
10．若定义在R上的函数f（x）满足f（0）=-1，其导函数f′（x） 满足f′（x）＞k＞1，则下列结论中一定正确的有①③
①$f（{\frac{1}{k}}）＞0$，②$f（{\frac{1}{k}}）＞\frac{k}{k-1}$，③$f（{\frac{1}{k-1}}）＞\frac{1}{k-1}$，④f（$\frac{1}{k-1}$）＞$\frac{k}{k-1}$．
11．已知直线y=k（x-1）（k＞0）与抛物线y2=4x交于A，B两点，若△AOB的面积为2$\sqrt{2}$，则|AB|=（　　）
A．2B．6C．4D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网