题目内容
11.已知a,b,c为圆O上的三点,若$\overrightarrow{OA}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=4,则|$\overrightarrow{AO}$|=$\frac{5}{2}$.分析 由题意和向量的运算可得BC为圆O的直径,进而由直径所对的圆周角为直角,即可求出半径.
解答  解:∵A,B,C是圆O上的三点,$\overrightarrow{OA}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,
解:∵A,B,C是圆O上的三点,$\overrightarrow{OA}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,
∴根据向量加法的运算,几何意义得出O为BC的中点,
即BC为圆O的直径,
∴圆周角∠CAB=90°
∴$\overrightarrow{AB}$和$\overrightarrow{AC}$的夹角为90°
∵|$\overrightarrow{AB}$|=3,|$\overrightarrow{AC}$|=4,
∴|$\overrightarrow{BC}$|=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴|$\overrightarrow{AO}$|=$\frac{1}{2}$|$\overrightarrow{BC}$|=$\frac{5}{2}$,
故答案为:$\frac{5}{2}$
点评 本题考查向量的夹角,涉及圆的知识,属基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
20.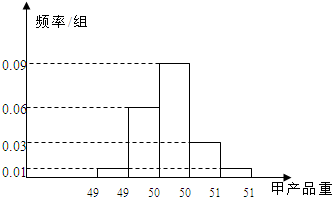 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
已知产品的重量合格标准为:重量值落在(495,510]内的产品为合格品;否则为不合格品.
(1)从甲流水线样本的合格品中任意取2件,求重量值落在(505,510]的产品件数X的分布列;
(2)从乙流水线中任取2件产品,试根据样本估计总体的思想,求其中合格品的件数Y的数学期望;
(3)从甲、乙流水线中各取2件产品,用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”,并用A表示事件“关于x的一元二次方程2x2+2ξx+ξ=0没有实数解”. 试根据样本估计总体的思想,求事件A的概率.
 某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:
某食品厂为了检查甲、乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本.经统计,得到关于产品重量的样本频率分布直方图和样本频数分布表:| 乙流水线 产品重量(单位:克) | 频数 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
(1)从甲流水线样本的合格品中任意取2件,求重量值落在(505,510]的产品件数X的分布列;
(2)从乙流水线中任取2件产品,试根据样本估计总体的思想,求其中合格品的件数Y的数学期望;
(3)从甲、乙流水线中各取2件产品,用ξ表示“甲流水线合格品数与乙流水线合格品数的差的绝对值”,并用A表示事件“关于x的一元二次方程2x2+2ξx+ξ=0没有实数解”. 试根据样本估计总体的思想,求事件A的概率.
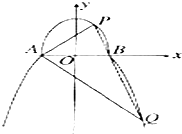 如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.
如图,曲线C由上半椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和部分抛物线C2:y=-x2+1(y≤0)连接而成,C1、C2的公共点为A,B,其中C1的离心率为$\frac{\sqrt{3}}{2}$.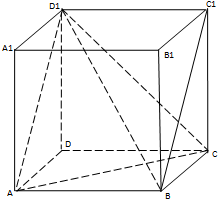 如图在正方体中
如图在正方体中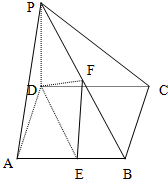 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点