题目内容
6.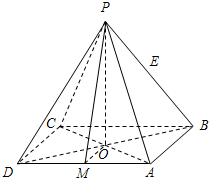 如图所示,四棱锥P-ABCD中,PA=PB=PC=PD,AB=a,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$.
如图所示,四棱锥P-ABCD中,PA=PB=PC=PD,AB=a,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$.(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值.
分析 (1)取AD中点M,连接MO,PM,则∠PMO为所求二面角P-AD-O的平面角,解得答案;
(2)连接AE,OE,则∠OEA为异面直线PD与AE所成的角,解得答案.
解答  解:(1)取AD中点M,连接MO,PM,
解:(1)取AD中点M,连接MO,PM,
依条件可知AD⊥MO,AD⊥PO,
则∠PMO为所求二面角P-AD-O的平面角.
∵PO⊥面ABCD,
∴∠PAO为侧棱PA与底面ABCD所成的角.
∴tan∠PAO=$\frac{{\sqrt{6}}}{2}$.
AB=a,AO=$\frac{{\sqrt{2}}}{2}$a,
∴PO=AO•tan∠POA=$\frac{{\sqrt{3}}}{2}$a,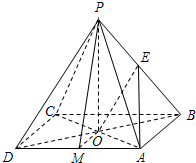
tan∠PMO=$\frac{PO}{MO}$=$\sqrt{3}$.
∴∠PMO=60°.…(6分)
(2)连接AE,OE,∵OE∥PD,
∴∠OEA为异面直线PD与AE所成的角.
∵AO⊥BD,AO⊥PO,∴AO⊥平面PBD.又OE?平面PBD,
∴AO⊥OE.
∵OE=$\frac{1}{2}$PD=$\frac{1}{2}$$\sqrt{{PO}^{2}+{DO}^{2}}$=$\frac{5}{4}$a,
∴tan∠AEO=$\frac{AO}{EO}$=$\frac{{2\sqrt{10}}}{5}$.…(12分)
点评 本题考查的知识点是二面角的平面角,异面直线的夹角,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.同时掷两个骰子,则向上的点数和为8的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{7}{36}$ | C. | $\frac{5}{36}$ | D. | $\frac{1}{4}$ |