题目内容
16.下列关于回归分析的说法正确的是④⑤(填上所有正确说法的序号)①相关系数r越小,两个变量的相关程度越弱;
②残差平方和越大的模型,拟合效果越好;
③用相关指数R2来刻画回归效果时,R2越小,说明模型的拟合效果越好;
④用最小二乘法求回归直线方程,是寻求使$\sum_{i=1}^n{{{({y_i}-b{x_i}-a)}^2}}$取最小值时的a,b的值;
⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
分析 可以用来衡量模拟效果好坏的几个量分别是相关指数,残差平方和和相关系数,只有残差平方和越小越好,其他的都是越大越好.
解答 解:①相关系数r的绝对值越趋近于1,相关性越强;越趋近于0,相关性越弱,故错误;
②残差平方和越小,模型拟合的效果越好,故错误;
③用相关指数R2来刻画回归效果时,R2越大,说明模型的拟合效果越好;
④用最小二乘法求回归直线方程,是寻求使$\sum_{i=1}^n{{{({y_i}-b{x_i}-a)}^2}}$取最小值时的a,b的值,根据用最小二乘法求回归直线方程的方法,可知正确;
⑤在残差图中,残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适,这样的带状区域的宽度越窄,模型拟合精度越高.
故答案为④⑤.
点评 本题主要考查线性相关指数的理解,解题的关键是理解对于拟合效果好坏的几个量的大小反映的拟合效果的好坏,比较基础.

练习册系列答案
相关题目
11.已知函数y=sin(2x-$\frac{π}{6}$)-m在[$\frac{π}{2}$,π]上有两个零点,则m的取值范围为( )
| A. | [$\frac{1}{2},1$] | B. | [-1,-$\frac{1}{2}$] | C. | [$\frac{1}{2},1$) | D. | (-1,-$\frac{1}{2}$] |
8.函数f(x)=4sin($\frac{1}{2}$x+$\frac{π}{6}$)的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
5. 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
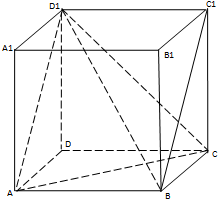 如图在正方体中
如图在正方体中