题目内容
13.已知f(x)=x3-$\frac{9}{2}$x2+6x-a,若对任意的x,f′(x)≥m恒成立,则m的最大值为( )| A. | 3 | B. | 2 | C. | 1 | D. | -$\frac{3}{4}$ |
分析 求出导函数,利用配方法求出导函数的最小值-$\frac{3}{4}$,得出答案.
解答 解:∵f(x)=x3-$\frac{9}{2}$x2+6x-a,
∴f'(x)=3x2-9x+6=3(x-$\frac{3}{2}$)2-$\frac{3}{4}$≥-$\frac{3}{4}$
∴m≤-$\frac{3}{4}$,
∴m的最大值为-$\frac{3}{4}$,
故选:D
点评 考查了导函数的求导,恒成立问题的转换.属于基础题型,应熟练掌握.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
8.函数f(x)=4sin($\frac{1}{2}$x+$\frac{π}{6}$)的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
5. 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
 如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )
如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点 在线段AC′上,若二面角A-BD-E与二面角E-BD-C′的大小分别为和45°和30°,则$\frac{AE}{EC′}$=( )| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
3.已知函数f(x)=2ax3-3ax2+1,g(x)=-$\frac{a}{4}x+\frac{3}{2}$,若对任意给定的m∈[0,2],关于x的方程f(x)=g(m)在区间[0,2]上总存在两个不同的解,则实数a的取值范围是( )
| A. | (-∞,-1) | B. | (1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | [-1,1] |
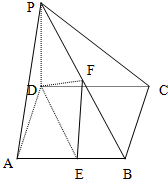 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方体,PD=CD=2,E、F分别是AB、PB的中点