题目内容
向量
，
，满足|
|=4，|
|=2，且（
-
）•
=0，则
与
的夹角（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：设
与
的夹角是θ，由题意和数量积的运算求出cosθ，再由向量的夹角范围求出θ的值．
| a |
| b |
解答：
解：设
与
的夹角是θ，
因为|
|=4，|
|=2，且（
-
）•
=0，
所以
•
-
•
=0，则4×2×cosθ-4=0，得cosθ=
，
又0≤θ≤π，所以θ=
，
故选：D．
| a |
| b |
因为|
| a |
| b |
| a |
| b |
| b |
所以
| a |
| b |
| b |
| b |
| 1 |
| 2 |
又0≤θ≤π，所以θ=
| π |
| 3 |
故选：D．
点评：本题考查数量积的运算，以及向量的夹角问题，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
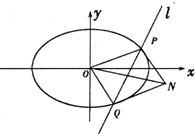已知椭圆C：
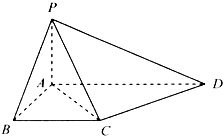如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是直角梯形，BC∥AD，∠ABC=90°，且PA=AB=BC=