题目内容
用综合法证明：若a＞0，b＞0，则
≥（
）3．
| a3+b3 |
| 2 |
| a+b |
| 2 |
考点：综合法与分析法(选修）
专题：证明题,综合法,推理和证明
分析：利用作差法，再与0比较，即可得出结论．
解答：
证明：
-（
）3=
（3a3+3b3-3a2b-3ab2）=
(a-b)2(a+b)，
∵a＞0，b＞0，
∴
(a-b)2(a+b)≥0，
∴
≥（
）3．
| a3+b3 |
| 2 |
| a+b |
| 2 |
| 1 |
| 8 |
| 3 |
| 8 |
∵a＞0，b＞0，
∴
| 3 |
| 8 |
∴
| a3+b3 |
| 2 |
| a+b |
| 2 |
点评：本题主要考查用综合法证明不等式，体现了转化的数学思想，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
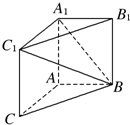如图，在三棱柱ABCA1B1C1中，AA1C1C是边长为4的正方形，平面ABC⊥平面AA1C1C，AB=3，BC=5．
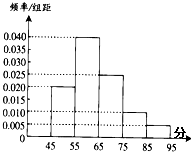为了调查某班学生做数学题的基本能力，随机抽查了部分学生某次做一份满分为100分的数学试题，他们所得分数的分组区间为[45，55），[55，65），[65，75），[75，85），[85，95），由此得到频率分布直方图如图，则这些学生的平均分为
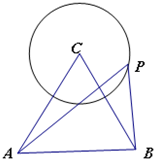如图，△ABC是边长为2
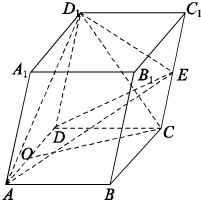已知斜四棱体ABCD-A1B1C1D1各棱长都是2，∠BAD=∠A1AD=60°，E、O分别是棱CC1和棱AD的中点，平面ADD1A1⊥平面ABCD．向量
，
，满足|
|=4，|
|=2，且（
-
）•
=0，则
与
的夹角（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
ρ=
（cosθ-sinθ）（ρ＞0）的圆心极坐标为（ ）
| 2 |
A、（-1，
| ||||
B、（1，
| ||||
C、（
| ||||
D、（1，
|