题目内容
已知向量
,
,
,
在平面上任选一点O,作
=
,
=
,
=
,
=
,则
=
+
+
+
=
+
+
+
.已知n个向量,依次把这n个向量首尾相连,以第一个向量的始点为始点,第n个向量的终点为终点的向量叫做 .
| a |
| b |
| c |
| d |
| OA |
| a |
| AB |
| b |
| BC |
| c |
| CD |
| d |
| OD |
| OA |
| AB |
| BC |
| CD |
| a |
| b |
| c |
| d |
考点:向量的三角形法则
专题:平面向量及应用
分析:利用向量的多边形法则即可得出.
解答:
解:把这n个向量首尾相连,以第一个向量的始点为始点,第n个向量的终点为终点的向量叫做这n个向量的和.
故答案为:这n个向量的和.
故答案为:这n个向量的和.
点评:本题考查了向量的多边形法则,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
向量
,
,满足|
|=4,|
|=2,且(
-
)•
=0,则
与
的夹角( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
ρ=
(cosθ-sinθ)(ρ>0)的圆心极坐标为( )
| 2 |
A、(-1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(1,
|
在定义域内满足f(x)•f(y)=f(x+y)的函数为( )
| A、f(x)=kx(k≠0) |
| B、f(x)=ax(a>0且a≠1) |
| C、f(x)=logax(a>0且a≠1) |
| D、f(x)=ax2+bx+c(a≠0) |
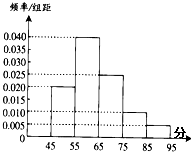 为了调查某班学生做数学题的基本能力,随机抽查了部分学生某次做一份满分为100分的数学试题,他们所得分数的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图,则这些学生的平均分为
为了调查某班学生做数学题的基本能力,随机抽查了部分学生某次做一份满分为100分的数学试题,他们所得分数的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图,则这些学生的平均分为