题目内容
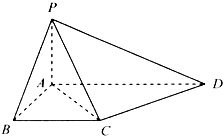 如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=
如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=| 1 |
| 2 |
(1)PB与CD所成的角的大小为
(2)PD与平面PAC所成角的余弦值为
(3)二面角B-PC-D的余弦值为
考点:二面角的平面角及求法,异面直线及其所成的角,直线与平面所成的角
专题:空间角
分析:(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出PB与CD所成的角的大小.
(2)求出平面PAC法向量,由此能求出PD与平面PAC所成角的余弦值.
(3)求出平面PBC的法向量和平面PCD的法向量,由此能求出二面角B-PC-D的余弦值.
(2)求出平面PAC法向量,由此能求出PD与平面PAC所成角的余弦值.
(3)求出平面PBC的法向量和平面PCD的法向量,由此能求出二面角B-PC-D的余弦值.
解答:
解: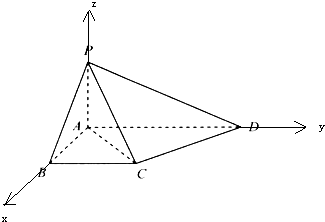 (1)以A为原点,AB为x轴,AD为y轴,AP为z轴,
(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,
建立空间直角坐标系,
则B(1,0,0),P(0,0,1),
C(1,1,0),D(0,2,0),
=(1,0,-1),
=(-1,1,0),
设PB与CD所成的角为α,
则cosα=|cos<
,
>|=
=
,
∴α=60°.
∴PB与CD所成的角的大小为60°.
(2)A(0,0,0),
=(0,2,-1),
=(0,0,1),
=(1,1,0),
设平面PAC法向量
=(x,y,z),
则
,取x=1,得
=(1,-1,0),
设PD与平面PAC所成角为θ,
则sinθ=|cos<
,
>|=
=
=
,
cosθ=
=
.
(3)
=(1,1,-1),
=(1,0,-1),
=(0,2,-1),
设平面PBC的法向量
=(a,b,c),
则
,取a=1,得
=(1,0,1),
设平面PCD的法向量
=(u,v,t),
则
,取v=1,得
=(1,1,2),
设二面角B-PC-D的平面角为β,
cosβ=
=
=
.
∴二面角B-PC-D的余弦值为
.
故答案为:60°;
;
.
 (1)以A为原点,AB为x轴,AD为y轴,AP为z轴,
(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
则B(1,0,0),P(0,0,1),
C(1,1,0),D(0,2,0),
| PB |
| CD |
设PB与CD所成的角为α,
则cosα=|cos<
| PB |
| CD |
|
| ||||
|
|
| 1 |
| 2 |
∴α=60°.
∴PB与CD所成的角的大小为60°.
(2)A(0,0,0),
| PD |
| AP |
| AC |
设平面PAC法向量
| n |
则
|
| n |
设PD与平面PAC所成角为θ,
则sinθ=|cos<
| PD |
| n |
|
| ||||
|
|
| 2 | ||||
|
| ||
| 5 |
cosθ=
1-(
|
| ||
| 5 |
(3)
| PC |
| PB |
| PD |
设平面PBC的法向量
| m |
则
|
| m |
设平面PCD的法向量
| p |
则
|
| p |
设二面角B-PC-D的平面角为β,
cosβ=
|
| ||||
|
|
| 3 | ||||
|
| ||
| 2 |
∴二面角B-PC-D的余弦值为
| ||
| 2 |
故答案为:60°;
| ||
| 5 |
| ||
| 2 |
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,线线角、线面角、二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
向量
,
,满足|
|=4,|
|=2,且(
-
)•
=0,则
与
的夹角( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
在定义域内满足f(x)•f(y)=f(x+y)的函数为( )
| A、f(x)=kx(k≠0) |
| B、f(x)=ax(a>0且a≠1) |
| C、f(x)=logax(a>0且a≠1) |
| D、f(x)=ax2+bx+c(a≠0) |
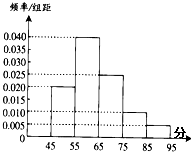 为了调查某班学生做数学题的基本能力,随机抽查了部分学生某次做一份满分为100分的数学试题,他们所得分数的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图,则这些学生的平均分为
为了调查某班学生做数学题的基本能力,随机抽查了部分学生某次做一份满分为100分的数学试题,他们所得分数的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95),由此得到频率分布直方图如图,则这些学生的平均分为 如图,△ABC是边长为2
如图,△ABC是边长为2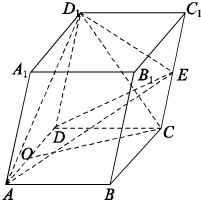 已知斜四棱体ABCD-A1B1C1D1各棱长都是2,∠BAD=∠A1AD=60°,E、O分别是棱CC1和棱AD的中点,平面ADD1A1⊥平面ABCD.
已知斜四棱体ABCD-A1B1C1D1各棱长都是2,∠BAD=∠A1AD=60°,E、O分别是棱CC1和棱AD的中点,平面ADD1A1⊥平面ABCD.