��Ŀ����
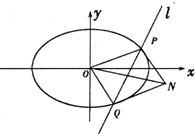 ��֪��ԲC��
��֪��ԲC��| x2 |
| a2 |
| y2 |
| b2 |
| �� |
| 4 |
| ||
| 2 |
| 3 |
��I������ԲC�ķ��̣�
������OP��OQΪ�ڱ���ƽ���ı���OQNP����ƽ���ı���OQNP���Ϊ
| 6 |
������������C2��y2=2px��p��0����F2Ϊ���㣬��������C2����ȡһ��S��S����ԭ��O������OSΪֱ����Բ����������C2����һ��R�����Բ�����Сʱ��S�����꣮
���㣺ֱ����Բ���ߵ��ۺ�����,��Բ�ı�����
ר�⣺Բ�����е���ֵ�뷶Χ����
��������I��ֱ��l����ԲC�ҽ���F2����б��Ϊ
ʱ���ɵ�ֱ��l�ķ���Ϊ��y=x-c����ԭ��O��ֱ��l�ľ���Ϊ
���ɵ�
=
�����c������Բ�ϵĵ㵽����F2���������Ϊ
-1���ɵ�a-c=
-1�����a��b2=a2-c2�����ɵó���ԲC�ķ��̣�
��II����P��x1��y1����Q��x2��y2������ֱ��l��б�ʲ�����ʱ��x1=x2��y1=-y2����
+
=1��|2x1•2y1|=
���ɵ�|ON|•|PQ|=2
����ֱ��l��б�ʴ���ʱ����ֱ��l�ķ���Ϊy=kx+m������Բ���������ɵã�2+3k2��x2+6kmx+3m2-6=0���ɡ���0�����3k2+2��m2�����ø���ϵ���Ĺ�ϵ�ɵ�|PQ|=
��ԭ�㵽ֱ��l�ľ���d=
������S��POQ=
d|PQ|=
����Ϊ3k2+2=2m2���������0����M��x0��y0��ΪPQ���е㣬�ɵ�|OM|2=
+
=
(3-
)��|PQ|2=2(2+
)���ɵ�|OM|2|PQ|2=(3-
)(2+
)�����û�������ʽ�����ʼ��ɵó���
��III��������ɵ�������C2��y2=4x������OSΪֱ����Բ����������C2����һ��R���ɵá�ORS=90�㣮�ɵ�
•
=0����S��x3��y3����R��x4��y4�����ɵ�y4��y4-y3��=-16�����û�������ʽ�����ʿɵ�y3��8����y3��-8��x3��16�����ɵó���
| �� |
| 4 |
| ||
| 2 |
| c | ||
|
| ||
| 2 |
| 3 |
| 3 |
��II����P��x1��y1����Q��x2��y2������ֱ��l��б�ʲ�����ʱ��x1=x2��y1=-y2����
| ||
| 3 |
| ||
| 2 |
| 6 |
| 6 |
| (1+k2)[(x1+x2)2-4x1x2] |
| |m| | ||
|
| 1 |
| 2 |
| ||
| 2 |
| x | 2 0 |
| y | 2 0 |
| 1 |
| 2 |
| 1 |
| m2 |
| 1 |
| m2 |
| 1 |
| m2 |
| 1 |
| m2 |
��III��������ɵ�������C2��y2=4x������OSΪֱ����Բ����������C2����һ��R���ɵá�ORS=90�㣮�ɵ�
| OR |
| SR |
���
�⣺��I��ֱ��l����ԲC�ҽ���F2����б��Ϊ
ʱ��
��ֱ��l�ķ���Ϊ��y=x-c��
��ԭ��O��ֱ��l�ľ���Ϊ
��
��
=
�����c=1��
����Բ�ϵĵ㵽����F2���������Ϊ
-1��
��a-c=
-1�����a=
��
��b2=a2-c2=2��
����ԲC�ķ���Ϊ
+
=1��
��II����P��x1��y1����Q��x2��y2����
�ٵ�ֱ��l��б�ʲ�����ʱ��x1=x2��y1=-y2��
��
+
=1��|2x1•2y1|=
�����|x1|=
��|y1|=1��
��|ON|•|PQ|=2
��
�ڵ�ֱ��l��б�ʴ���ʱ����ֱ��l�ķ���Ϊy=kx+m��
����
������2+3k2��x2+6kmx+3m2-6=0��
�ɡ���0�����3k2+2��m2��
��x1+x2=-
��x1x2=
��
��|PQ|=
=
��
ԭ�㵽ֱ��l�ľ���d=
��
��S��POQ=
d|PQ|=
=
��
��Ϊ3k2+2=2m2���������0��
��M��x0��y0��ΪPQ���е㣬��x0=
=-
��y0=kx0+m=
��
��|OM|2=
+
=
+
=
(3-
)��|PQ|2=2(2+
)��
��|OM|2|PQ|2=(3-
)(2+
)��
�����ҽ���m=��
ʱȡ�Ⱥţ�
��|OM||PQ|�����ֵΪ
��
��|ON|•|PQ|=2|OM||PQ|�����ֵΪ5��
���Ͽɵã�ON|•|PQ|�����ֵΪ5��
��III��������ɵ�������C2��y2=4x��
����OSΪֱ����Բ����������C2����һ��R�����ORS=90�㣮��
•
=0��
��S��x3��y3����R��x4��y4����
��
•
=x4��x4-x3��+y4��y4-y3��=
+y4��y4-y3��=0��
��y4��y4-y3����0����y4��y4-y3��=-16��
��y3=
+y4��8����y3��-8
x3��
=16��
���Բ�����Сʱ��S������Ϊ��16����8����
| �� |
| 4 |
��ֱ��l�ķ���Ϊ��y=x-c��
��ԭ��O��ֱ��l�ľ���Ϊ
| ||
| 2 |
��
| c | ||
|
| ||
| 2 |
����Բ�ϵĵ㵽����F2���������Ϊ
| 3 |
��a-c=
| 3 |
| 3 |
��b2=a2-c2=2��
����ԲC�ķ���Ϊ
| x2 |
| 3 |
| y2 |
| 2 |
��II����P��x1��y1����Q��x2��y2����
�ٵ�ֱ��l��б�ʲ�����ʱ��x1=x2��y1=-y2��
��
| ||
| 3 |
| ||
| 2 |
| 6 |
| ||
| 2 |
��|ON|•|PQ|=2
| 6 |
�ڵ�ֱ��l��б�ʴ���ʱ����ֱ��l�ķ���Ϊy=kx+m��
����
|
�ɡ���0�����3k2+2��m2��
��x1+x2=-
| 6km |
| 2+3k2 |
| 3m2-6 |
| 2+3k2 |
��|PQ|=
| (1+k2)[(x1+x2)2-4x1x2] |
2
| ||||||
| 2+3k2 |
ԭ�㵽ֱ��l�ľ���d=
| |m| | ||
|
��S��POQ=
| 1 |
| 2 |
| ||||
| 2+3k2 |
| ||
| 2 |
��Ϊ3k2+2=2m2���������0��
��M��x0��y0��ΪPQ���е㣬��x0=
| x1+x2 |
| 2 |
| 3k |
| 2m |
| 1 |
| m |
��|OM|2=
| x | 2 0 |
| y | 2 0 |
| 9k2 |
| 4m2 |
| 1 |
| m2 |
| 1 |
| 2 |
| 1 |
| m2 |
| 1 |
| m2 |
��|OM|2|PQ|2=(3-
| 1 |
| m2 |
| 1 |
| m2 |
| 25 |
| 4 |
| 2 |
��|OM||PQ|�����ֵΪ
| 5 |
| 2 |
��|ON|•|PQ|=2|OM||PQ|�����ֵΪ5��
���Ͽɵã�ON|•|PQ|�����ֵΪ5��
��III��������ɵ�������C2��y2=4x��
����OSΪֱ����Բ����������C2����һ��R�����ORS=90�㣮��
| OR |
| SR |
��S��x3��y3����R��x4��y4����
��
| OR |
| SR |
| ||||||
| 16 |
��y4��y4-y3����0����y4��y4-y3��=-16��
��y3=
| 16 |
| y4 |
x3��
| ||
| 4 |
���Բ�����Сʱ��S������Ϊ��16����8����
���������⿼������Բ�������ߵı����̼������ʡ�ֱ������Բ�ཻ����ת��Ϊ���������ɵá���0�������ϵ���Ĺ�ϵ���ҳ���ʽ���㵽ֱ�ߵľ��빫ʽ�������ε�������㹫ʽ����������ʽ�����ʣ���������������������������������⣮

��ϰ��ϵ�д�
�����Ŀ
���P������y=x2�ϣ���Q��ֱ��y=2x-2�ϣ���PQ����СֵΪ��������
A��
| ||||
B��
| ||||
C��
| ||||
D��
|
����
��
������|
|=4��|
|=2���ң�
-
��•
=0����
��
�ļнǣ�������
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
A��
| ||
B��
| ||
C��
| ||
D��
|
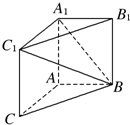 ��ͼ����������ABCA1B1C1�У�AA1C1C�DZ߳�Ϊ4�������Σ�ƽ��ABC��ƽ��AA1C1C��AB=3��BC=5��
��ͼ����������ABCA1B1C1�У�AA1C1C�DZ߳�Ϊ4�������Σ�ƽ��ABC��ƽ��AA1C1C��AB=3��BC=5��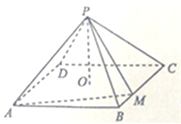 ��ͼ������P-ABCD�У���������OΪ���ĵ����Σ�PO�͵���ABCD��PO=
��ͼ������P-ABCD�У���������OΪ���ĵ����Σ�PO�͵���ABCD��PO=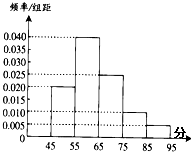 Ϊ�˵���ij��ѧ������ѧ��Ļ����������������˲���ѧ��ij����һ������Ϊ100�ֵ���ѧ���⣬�������÷����ķ�������Ϊ[45��55����[55��65����[65��75����[75��85����[85��95�����ɴ˵õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ������Щѧ����ƽ����Ϊ
Ϊ�˵���ij��ѧ������ѧ��Ļ����������������˲���ѧ��ij����һ������Ϊ100�ֵ���ѧ���⣬�������÷����ķ�������Ϊ[45��55����[55��65����[65��75����[75��85����[85��95�����ɴ˵õ�Ƶ�ʷֲ�ֱ��ͼ��ͼ������Щѧ����ƽ����Ϊ