题目内容
已知
=(cosx,-
),
=(sinx+cosx,1),f(x)=
•
,
(Ⅰ)若0<α<
,sinα=
,求f(α)的值;
(Ⅱ)求函数f(x)的最小正周期及单调递增区间.
| a |
| 1 |
| 2 |
| b |
| a |
| b |
(Ⅰ)若0<α<
| π |
| 2 |
| ||
| 2 |
(Ⅱ)求函数f(x)的最小正周期及单调递增区间.
考点:平面向量数量积的运算,三角函数的周期性及其求法,正弦函数的图象
专题:三角函数的求值,三角函数的图像与性质,平面向量及应用
分析:( I)由条件可得α=
,再由向量的数量积的坐标表示和二倍角公式及两角和的正弦公式,化简f(x),再代入计算即可得到所求值;
( II)运用正弦函数的周期公式和增区间,解不等式即可得到最小正周期和所求增区间.
| π |
| 4 |
( II)运用正弦函数的周期公式和增区间,解不等式即可得到最小正周期和所求增区间.
解答:
解:( I)由0<α<
,sinα=
,则α=
,
由
=(cosx,-
),
=(sinx+cosx,1),
则f(x)=
•
=cosxsinx+cos2x-
=
sin2x+
cos2x
=
sin(2x+
),
即有f(α)=
sin(2×
+
)=
×
=
;
( II)由( I)可得,f(x)=
sin(2x+
),
则f(x)的最小正周期T=
=π;
由2kπ-
≤2x+
≤2kπ+
, k∈Z,
解得kπ-
≤x≤kπ+
, k∈Z,
则f(x)的单调增区间为[kπ-
, kπ+
], k∈Z.
| π |
| 2 |
| ||
| 2 |
| π |
| 4 |
由
| a |
| 1 |
| 2 |
| b |
则f(x)=
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 2 |
| π |
| 4 |
即有f(α)=
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
( II)由( I)可得,f(x)=
| ||
| 2 |
| π |
| 4 |
则f(x)的最小正周期T=
| 2π |
| 2 |
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得kπ-
| 3π |
| 8 |
| π |
| 8 |
则f(x)的单调增区间为[kπ-
| 3π |
| 8 |
| π |
| 8 |
点评:本题考查向量的数量积的坐标表示和二倍角公式及两角和的正弦公式的运用,主要考查正弦函数的周期公式和单调区间,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
设点P在曲线y=x2上,点Q在直线y=2x-2上,则PQ的最小值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
向量
,
,满足|
|=4,|
|=2,且(
-
)•
=0,则
与
的夹角( )
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
ρ=
(cosθ-sinθ)(ρ>0)的圆心极坐标为( )
| 2 |
A、(-1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(1,
|
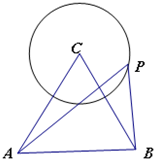 如图,△ABC是边长为2
如图,△ABC是边长为2