题目内容
3.已知直线y=x-2与抛物线y2=2x相交于A、B两点,O为坐标原点.(1)求证:OA⊥OB.
(2)求|AB|.
分析 (1)将直线方程代入抛物线方程,利用韦达定理,求得y1y2及x1x2,由$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=0,即可证明OA⊥OB;
(2)利用弦长公式即可求得|AB|.
解答 解:(1)证明:设A(x1,y1 ),B(x2,y2),
则$\left\{\begin{array}{l}{y=x-2}\\{{y}^{2}=2x}\end{array}\right.$,整理得:y2-2y-4=0,
∴y1+y2=2,y1y2=-4
∴x1x2=(y1+2)(y2+2)=y1y2+2(y1+y2)+4=4,
由$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=4+(-4)=0,
∴$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,
∴OA⊥OB.
(2)由(1)可知:x1+x2=(y1+2)+(y2+2)=y1+y2+4=6,
|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$•$\sqrt{36-4×4}$=2$\sqrt{10}$,
∴|AB|=2$\sqrt{10}$.
点评 本题考查直线与抛物线的位置关系,考查韦达定理,弦长公式,考查计算能力,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
14.如果实数x、y满足关系$\left\{\begin{array}{l}{x+y-2≤0}\\{x-y≤0}\\{2x-y+2≥0}\end{array}\right.$则(x-1)2+y2的最小值是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\sqrt{2}$ |
15.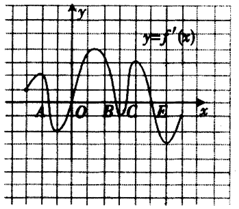 函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )
函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )
 函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )
函数y=f(x)定义在区间(-3,7)上,其导函数如图所示,则函数y=f(x)在区间(-3,7)上极小值的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.已知直线l:x+ay-1=0(a∈R)是圆C:x2+y2-4x-2y+1=0的对称轴,过点A(-4,a)作圆C的一条切线,切点为B,则|AB|=( )
| A. | 2 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{10}$ | D. | 6 |