题目内容

15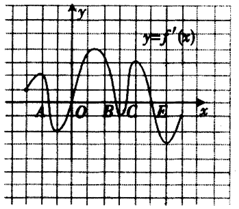．函数y=f（x）定义在区间（-3，7）上，其导函数如图所示，则函数y=f（x）在区间（-3，7）上极小值的个数是（　　）
A．2个B．3个C．4个D．5个

分析 函数在极小值点处，导数为0，且导函数左负右正，根据图象可得结论．

解答 解：函数在极小值点处，导数为0，且导函数左负右正，
根据图象可知，O，C为极小值点，
故选：A．

点评 本题以导函数的图象为载体，考查函数的极值，解题的关键是函数在极小值点处，导数为0，且导函数左负右正．

练习册系列答案
相关题目
3．复数$\frac{5i}{1+2i}$的虚部是（　　）
A．iB．-iC．1D．-1
6．已知函数f（x）=ex+x3，若f（x2）＜f（3x-2），则实数x的取值范围是（1，2）．
3．已知直线y=x-2与抛物线y2=2x相交于A、B两点，O为坐标原点．
（1）求证：OA⊥OB．
（2）求|AB|．
10．已知方程x2+my2=1表示焦点在y轴上的椭圆，则m的取值范围是（　　）
A．m＜1B．-1＜m＜1C．m＞1D．0＜m＜1
20．已知$\overrightarrow{a}$=（$\sqrt{3}$sinωx，cosωx），$\overrightarrow{b}$=（cosωx，cosωx）（ω＞0），记函数f（x）=$\vec a$•$\vec b$，且f（x）的最小正周期是π，则ω=（　　）
A．ω=1B．ω=2C．ω=$\frac{1}{2}$D．ω=$\frac{2}{3}$
7．如果质点A按照规律s=3t2运动，则在t0=3时的瞬时速度为（　　）
A．12B．16C．18D．27
4．设是定义在R上的偶函数，且f（x+2）=f（2-x）时，当x∈[-2，0]时，$f（x）={（\frac{{\sqrt{2}}}{2}）^x}-1$，若（-2，6）在区间内关于x的方程xf（x）-loga（x+2）=0（a＞0且a≠1）有且只有4个不同的根，则实数a的范围是（　　）
A．$（\frac{1}{4}，1）$B．（1，4）C．（1，8）D．（8，+∞）
5．若函数f（a）=$\int_0^a{（{2+sinx}）dx}$，则$f（{\frac{π}{2}}）$等于（　　）
A．1B．0C．π+1D．1-cos1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网