题目内容
6.给出下列五个命题:①函数y=2sin(2x-$\frac{π}{3}$)的一条对称轴是x=$\frac{5π}{12}$
②函数y=tanx的图象关于点($\frac{π}{2}$,0)对称;
③正弦函数在第一象限为增函数;
以上三个命题中正确的有①②(填写所有正确命题的序号)
分析 求出当x=$\frac{5π}{12}$时,函数y=2sin(2x-$\frac{π}{3}$)的值判断①;由正切函数的图象判断②;举例说明③错误.
解答 解:当x=$\frac{5π}{12}$时,函数y=2sin(2x-$\frac{π}{3}$)的值为2sin($2×\frac{5π}{12}-\frac{π}{3}$)=2,∴函数y=2sin(2x-$\frac{π}{3}$)的一条对称轴是x=$\frac{5π}{12}$,故①正确;
由正切函数的图象可知,函数y=tanx的图象关于点($\frac{π}{2}$,0)对称,故②正确;
∵390°>60°,但sin390°<sin60°,∴正弦函数在第一象限不是增函数,故③错误.
∴正确命题的序号是①②.
故答案为:①②.
点评 本题考查命题的真假判断与应用,考查三角函数的图象和性质,是基础题.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
17.在△ABC中,AB=3,BC=4,D是BC的中点,且$∠B=\frac{π}{3}$,则sin∠ADC=( )
| A. | $\frac{{\sqrt{7}}}{4}$ | B. | $\frac{{3\sqrt{21}}}{14}$ | C. | $\frac{{\sqrt{39}}}{26}$ | D. | $\frac{{\sqrt{7}}}{28}$ |
1.在数列{an}中,a1=2,an+1=an+lg(1+$\frac{1}{n}$),则an的值为( )
| A. | 2+lgn | B. | 2+(n-1)lgn | C. | 2+nlgn | D. | 1+nlgn |
11.设函数f(x)为定义域为R的奇函数,且f(x)=f(2-x),当x∈[0,1]时,f(x)=sinx,则函数g(x)=|cos(πx)|-f(x)在区间$[-\frac{5}{2},\frac{9}{2}]$上的所有零点的和为( )
| A. | 6 | B. | 7 | C. | 13 | D. | 14 |
18.若圆的一条直径的两个端点分别是(2,0)和(2,-2),则此圆的方程是( )
| A. | x2+y2-4x+2y+4=0 | B. | x2+y2-4x-2y-4=0 | C. | x2+y2-4x+2y-4=0 | D. | x2+y2+4x+2y+4=0 |
16.三棱锥A-BCD内接于半径为2的球O,BC过球心O,当三棱锥A-BCD体积取得最大值时,三棱锥A-BCD的表面积为( )
| A. | $6+4\sqrt{3}$ | B. | $8+2\sqrt{3}$ | C. | $4+6\sqrt{3}$ | D. | $8+4\sqrt{3}$ |
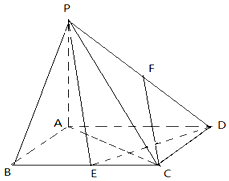 如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.
如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.