题目内容
14.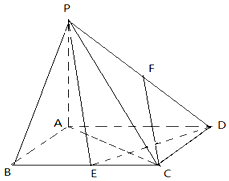 如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.
如图,四棱锥P-ABCD的底面是矩形,PA⊥底面ABCD,PA=AD=2AB=2,E、F分别为BC与PD的中点.(1)求证:PE⊥DE;
(2)求直线CF与平面PAC的夹角θ的余弦值.
分析 (1)建立空间直角坐标系,利用向量的方法证明:PE⊥DE;
(2)求出面PAC的法向量,即可求直线CF与平面PAC的夹角θ的余弦值.
解答  解:(1)如图建立空间直角坐标系,则P(0,0,2),E(1,1,0),D(0,2,0),
解:(1)如图建立空间直角坐标系,则P(0,0,2),E(1,1,0),D(0,2,0),
∴$\overrightarrow{PE}$=(1,1,-2),$\overrightarrow{DE}$=(1,-1,0),
∵$\overrightarrow{PE}•\overrightarrow{DE}$=0,
∴PE⊥DE …(5分)
(2)C(1,2,0)F(0,1,1)A(0,0,0)设面PAC的法向量为$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}\overrightarrow{AP}•\overrightarrow n=0\\ \overrightarrow{AC}•\overrightarrow n=0\end{array}\right.$得$\left\{\begin{array}{l}z=0\\ x+2y=0\end{array}\right.$取$\overrightarrow{n}$=(2,-1,0)
又∵$\overrightarrow{CF}$=(-1,-1,1)…(8分)
∴$sinθ=|{cos<\overrightarrow{CF},\overrightarrow n>}|=\frac{1}{{\sqrt{3}•\sqrt{5}}}=\frac{1}{{\sqrt{15}}}$…(11分)
即知$cosθ=\frac{{\sqrt{14}}}{{\sqrt{15}}}=\frac{{\sqrt{210}}}{15}$…(12分)
点评 本题考查向量方法的运用,考查线线垂直,线面角,考查学生分析解决问题的能力,属于中档题.

| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{{\sqrt{3}π}}{9}$ | D. | $\frac{π}{6}$ |
| A. | 51 | B. | 34 | C. | 102 | D. | 不能确定 |
