题目内容

1．在数列{an}中，a1=2，an+1=an+lg（1+$\frac{1}{n}$），则an的值为（　　）
A．2+lgnB．2+（n-1）lgnC．2+nlgnD．1+nlgn

分析 首先根据已知条件，利用递推关系整理出多个关系式，观察规律，整理出通项公式．

解答 解：已知：an+1=an+lg（1+$\frac{1}{n}$）①
an=an-1+lg（1+$\frac{1}{n-1}$） ②
…
a2=a1+lg（1+$\frac{1}{1}$）（n）
①+②+…+（n）得：
an=a1+lg（2•$\frac{3}{2}$•$\frac{4}{3}$•…$\frac{n}{n-1}$）
因为：a1=2
所以：an=2+lgn，
故选：A．

点评 本题考查的知识点：用数列的递推关系式求通项公式，对数的运算法则的应用，考查计算能力．

练习册系列答案
相关题目
11．数列{an}，a1=2，an=2an-1+2n（n≥2）
（I）求证数列{$\frac{{a}_{n}}{{2}^{n}}$}是等差数列；
（II）求数列{an}的前n项和Sn；
（III）若bn=$\frac{2n-1}{{a}_{n}}$，求证数列{bn}为递减数列．
12．已知矩形ABCD的周长为18，把它沿图中的虚线折成正四棱柱，则这个正四棱柱的外接球表面积的最小值为36π．
9．已知函数f（x）=lnx，h（x）=ax（a∈R）．
（1）函数f（x）的图象与h（x）的图象无公共点，求实数a的取值范围；
（2）是否存在实数m，使得对任意的$x∈（{\frac{1}{2}，+∞}）$，都有函数y=f（x）+$\frac{m}{x}$的图象在$g（x）={\frac{ex}{x}^{\;}}$的图象的下方？若存在，求出整数m的最大值；若不存在，请说明理由．（$\sqrt{e}+\frac{1}{2}$ln2≈1.99）
16．已知向量$\overrightarrow a，\;\overrightarrow b，\;\overrightarrow c$是同一平面内的三个向量，其中$\overrightarrow a=（{1，\;2}）$．
（1）若$|{\overrightarrow c}|=2\sqrt{5}$，且向量$\overrightarrow c$与向量$\overrightarrow a$反向，求$\overrightarrow c$的坐标；
（2）若$|{\overrightarrow b}|=\frac{{\sqrt{5}}}{2}$，且$（\overrightarrow a+2\overrightarrow b）•（2\overrightarrow a-\overrightarrow b）=\frac{15}{4}$，求$\overrightarrow a$在$\overrightarrow b$方向上的射影．
6．给出下列五个命题：
①函数y=2sin（2x-$\frac{π}{3}$）的一条对称轴是x=$\frac{5π}{12}$
②函数y=tanx的图象关于点（$\frac{π}{2}$，0）对称；
③正弦函数在第一象限为增函数；
以上三个命题中正确的有①②（填写所有正确命题的序号）
13．已知α，β是两个不同的平面，m，n是两条不同的直线，则下列五个命题：
①如果m⊥α，n∥β，α∥β，那么m⊥n；
②如果m∥α，n∥β，m⊥n，那么α∥β；
③如果m⊥α，n⊥β，m⊥n，那么α⊥β；
④如果m⊥α，n∥β，m⊥n，那么α∥β；
⑤如果m∥α，m∥β，α∩β=n，那么m∥n．
其中正确的命题有①③⑤．（填写所有正确命题的编号）
10．设函数f（x）=x2-alnx，g（x）=（a-2）x
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若函数F（x）=f（x）-g（x）有两个零点x1，x2
（1）求满足条件的最小正整数a的值；
（2）求证：F′（$\frac{{x}_{1}+{x}_{2}}{2}$）＞0．
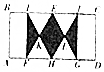11．如图所示，已知长方形ABCD中，BC=2AB，△EFG与△HIJ均为等边三角形，F、H、G在AD上，I、E、J在BC上，连接FI，GJ，且AB∥FI∥GJ，若AF=GD，则向长方形ABCD内投掷一个点，该点落在阴影区域内的概率为$\frac{\sqrt{3}}{6}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网