题目内容
11.设函数f(x)为定义域为R的奇函数,且f(x)=f(2-x),当x∈[0,1]时,f(x)=sinx,则函数g(x)=|cos(πx)|-f(x)在区间$[-\frac{5}{2},\frac{9}{2}]$上的所有零点的和为( )| A. | 6 | B. | 7 | C. | 13 | D. | 14 |
分析 确定函数的周期为4,且y=f(x)的图象关于直线x=1对称,g(x)=|cos(πx)|-f(x)在区间$[{-\frac{5}{2},\;\;\frac{9}{2}}]$上的零点,即方程|cos(πx)|=f(x)的零点,利用图象可得结论.
解答 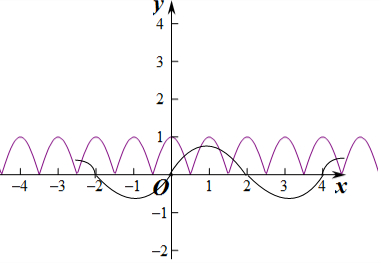 解:由题意,函数f(-x)=-f(x),f(x)=f(2-x),则-f(-x)=f(2-x),可得f(x+4)=f(x),即函数的周期为4,
解:由题意,函数f(-x)=-f(x),f(x)=f(2-x),则-f(-x)=f(2-x),可得f(x+4)=f(x),即函数的周期为4,
且y=f(x)的图象关于直线x=1对称.
g(x)=|cos(πx)|-f(x)在区间$[{-\frac{5}{2},\;\;\frac{9}{2}}]$上的零点,即方程|cos(πx)|=f(x)的零点,
画y=|cos(πx)|函数图象,
∵两个函数的图象都关于直线x=1对称,
∴方程|cos(πx)|=f(x)的零点关于直线x=1对称,
由图象可知交点个数为6个,可得所有零点的和为6,
故选A.
点评 本题考查函数的图象与性质,考查学生分析解决问题的能力,正确转化是关键.

练习册系列答案
相关题目
2.在等差数列中,a9=3,则此数列前17项和等于( )
| A. | 51 | B. | 34 | C. | 102 | D. | 不能确定 |
16.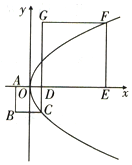 如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
 如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )
如图所示,正方形ABCD和正方形DEFG,原点O为AD的中点,抛物线y2=2px(p>0)经过C,F两点,则直线BE的斜率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $1-\frac{{\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $2-\sqrt{2}$ |
1. 如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )
如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )
 如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )
如图,有一个水平放置的透明无盖的正三棱柱容器,其中侧棱长为8cm,底面边长为12cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时,测得水深为6cm,如果不计容器的厚度,则球的表面积为( )| A. | 36πcm2 | B. | 64πcm2 | C. | 80πcm2 | D. | 100πcm2 |
