题目内容
深圳科学高中大约共有600台空调，空调运行所释放的氟里昂会破坏大气上层的臭氧层．假设臭氧层含量W呈指数型函数变化，满足关系W=W0e-0.02t，其中W0是臭氧的初始量．（参考数据 e-0.6932=
）
（1）判断函数W=W0e-0.02t的单调性，并用定义证明．
（2）多少年后将会有一半的臭氧消失？
| 1 |
| 2 |
（1）判断函数W=W0e-0.02t的单调性，并用定义证明．
（2）多少年后将会有一半的臭氧消失？
考点：函数模型的选择与应用
专题：应用题,函数的性质及应用
分析：（1）利用函数的单调性的定义，即可证明；
（2）一半的臭氧消失时，W=
W0，即可得出结论．
（2）一半的臭氧消失时，W=
| 1 |
| 2 |
解答：
解：（1）函数W=W0e-0.02t的定义域为[0，+∞），在[0，+∞）上为减函数．…（2分）
证明：对任意的t1，t2∈[0，+∞）且t1＜t2，有 …（3分）
=
=(e-0.02)t1-t2．…（5分）
又t2＞t1≥0，所以t1-t2＜0，
又0＜e-0.02＜1，所以(e-0.02)t1-t2＞1，即W1＞W2．…（7分）
所以，函数W=W0e-0.02t在[0，+∞）上为减函数．…（8分）
（2）一半的臭氧消失时，W=
W0，所以 …（9分）
W=W0e-0.02t=
W0，e-0.02t=
=e-0.06932，
解得，t=34.66．…（11分）
即34.66年后，将会有一半的臭氧消失．…（12分）
证明：对任意的t1，t2∈[0，+∞）且t1＜t2，有 …（3分）
| W1 |
| W2 |
| W0e-0.02t1 |
| W0e-0.02t2 |
又t2＞t1≥0，所以t1-t2＜0，
又0＜e-0.02＜1，所以(e-0.02)t1-t2＞1，即W1＞W2．…（7分）
所以，函数W=W0e-0.02t在[0，+∞）上为减函数．…（8分）
（2）一半的臭氧消失时，W=
| 1 |
| 2 |
W=W0e-0.02t=
| 1 |
| 2 |
| 1 |
| 2 |
解得，t=34.66．…（11分）
即34.66年后，将会有一半的臭氧消失．…（12分）
点评：本题考查函数的选择与应用，考查函数的单调性，考查学生的计算能力，属于中档题．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
在等差数列{an}中，a1=1，a3=5，则a5=（ ）
| A、3 | B、5 | C、7 | D、9 |
若a，b，c∈C（C为复数集），则（a-b）2+（b-c）2=0是a=b=c的（ ）
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
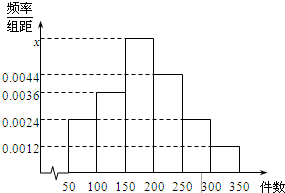从某工厂抽取50名工人进行调查，发现他们一天加工零件的个数在50至350个之间，现按生产的零件个数将他们分成六组，第一组[50，100），第二组[100，150），第三组[150，200），第四组[200，250），第五组[200，250），第六组[300，350），相应的样本频率分布直方图如图所示：