题目内容
在从2011年到2014年期间,甲每年1月1日都到银行存入a元的一年定期储蓄.若年利率为q保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
| A、a(1+q)4 | ||
| B、a(1+q)5 | ||
C、
| ||
D、
|
考点:等比数列的前n项和
专题:等差数列与等比数列
分析:先分别计算每一年存入a元到2011年的本息和,然后将所有存款的本息相加,根据等比数列求得求和公式解之即可.
解答:
解:2011年的a元到了2014年本息和为a(1+q)3,
2012年的a元到了2014年本息和为a(1+q)2,
2013年的a元到了2014年本息和为a(1+q),
所有金额为a(1+q)+a(1+q)2+a(1+q)3
即所有金额为
=
故选:C.
2012年的a元到了2014年本息和为a(1+q)2,
2013年的a元到了2014年本息和为a(1+q),
所有金额为a(1+q)+a(1+q)2+a(1+q)3
即所有金额为
| a(1+q)[1-(1+q)3] |
| 1-(1-q) |
| a[(1+q)4-(1-q)] |
| q |
故选:C.
点评:本题主要考查了数列的应用,以及等比数列的求和,同时考查了计算能力,属于中档题.

练习册系列答案
相关题目
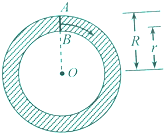 如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×
如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×| R+r |
| 2 |
| R+r |
| 2 |
| A、2πr2d |
| B、2π2r2d |
| C、2πrd2 |
| D、2π2rd2 |
已知圆锥的母线长为8,底面周长为6π,则它的体积为( )
A、9
| ||
B、9
| ||
C、3
| ||
D、3
|
在独立性检验中,统计量Χ2有两个临界值:3.841和6.635;当Χ2>3.841时,有95%的把握说明两个事件有关,当Χ2>6.635时,有99%的把握说明两个事件有关,当Χ2≤3.841时,认为两个事件无关.调查者通过询问50名男女大学生在选修课程时是否选择“统计学”课程,得到数据如下表:
根据表中的数据,得到Χ2=
≈4.844.根据这一数据分析,认为大学生的性别和是否选修“统计学”课程之间( )
| 不选统计学 | 选统计学 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| 50×(13×20-10×7)2 |
| 23×27×20×30 |
| A、有95%的把握认为两者有关 |
| B、约有95%的选修“统计学”课程的学生是女性 |
| C、有99%的把握认为两者有关 |
| D、约有99%的选修“统计学”课程的学生是女性 |
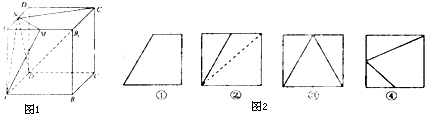
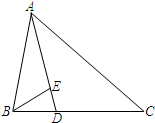 如图,在△ABC中,已知∠BAC=
如图,在△ABC中,已知∠BAC=