题目内容
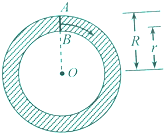 如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×
如图,我们知道,圆环也可看作线段AB绕圆心O旋转一周所形成的平面图形,又圆环的面积S=π(R2-r2)=(R-r)×2π×| R+r |
| 2 |
| R+r |
| 2 |
| A、2πr2d |
| B、2π2r2d |
| C、2πrd2 |
| D、2π2rd2 |
考点:旋转体(圆柱、圆锥、圆台)
专题:简易逻辑
分析:根据已知中圆环的面积等于是以线段AB=R-r为宽,以AB中点绕圆心O旋转一周所形成的圆的周长2π×
为长的矩形面积.拓展到空间后,将平面区域M={(x,y)|(x-d)2+y2≤r2}(其中0<r<d)绕y轴旋转一周,则所形成的旋转体的体积应等于:以圆(x-d)2+y2=r2为底面,以圆心(d,0)绕y轴旋转一周形成的圆的周长2π×d为高的圆柱的体积.代入可得答案.
| R+r |
| 2 |
解答:
解:由已知中圆环的面积等于是以线段AB=R-r为宽,
以AB中点绕圆心O旋转一周所形成的圆的周长2π×
为长的矩形面积.
拓展到空间后,将平面区域M={(x,y)|(x-d)2+y2≤r2}(其中0<r<d)绕y轴旋转一周,
则所形成的旋转体的体积应等于:
以圆(x-d)2+y2=r2为底面,以圆心(d,0)绕y轴旋转一周形成的圆的周长2π×d为高的圆柱的体积.
故V=πr2•2πd=2π2r2d,
故选:B
以AB中点绕圆心O旋转一周所形成的圆的周长2π×
| R+r |
| 2 |
拓展到空间后,将平面区域M={(x,y)|(x-d)2+y2≤r2}(其中0<r<d)绕y轴旋转一周,
则所形成的旋转体的体积应等于:
以圆(x-d)2+y2=r2为底面,以圆心(d,0)绕y轴旋转一周形成的圆的周长2π×d为高的圆柱的体积.
故V=πr2•2πd=2π2r2d,
故选:B
点评:本题考查的知识点是圆柱的体积,类比推理,其中得到拓展到空间后,将平面区域M={(x,y)|(x-d)2+y2≤r2}(其中0<r<d)绕y轴旋转一周,则所形成的旋转体的体积应等于:以圆(x-d)2+y2=r2为底面,以圆心(d,0)绕y轴旋转一周形成的圆的周长2π×d为高的圆柱的体积.是解答的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
在从2011年到2014年期间,甲每年1月1日都到银行存入a元的一年定期储蓄.若年利率为q保持不变,且每年到期的存款本息均自动转为新的一年定期储蓄,到2014年1月1日,甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )元.
| A、a(1+q)4 | ||
| B、a(1+q)5 | ||
C、
| ||
D、
|
若角α的终边经过点P(1,-2),则sinα=( )
A、
| ||||
B、-
| ||||
| C、-2 | ||||
D、-
|
下列命题正确的是( )
| A、以直角三角形的一直角边为轴旋转所得的旋转体是圆锥 |
| B、以直角梯形的一腰为轴旋转所得的旋转体是圆台 |
| C、圆柱、圆锥、圆台都有两个底面 |
| D、圆锥的侧面展开图为扇形,此扇形所在圆的半径等于圆锥底面圆半径 |
与角-80°终边相同的角是( )
| A、80° | B、100° |
| C、260° | D、280° |
设a∈R,则“a=-1”是“直线ax+y-1=0与直线x+y+5=0垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
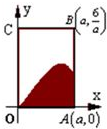 如图,矩形OABC内阴影部分是由曲线f(x)=sinx(x∈(0,π)及直线x=a(a∈(0,π)与x轴围成,向矩形OABC内随机的投掷一点,若落在阴影部分的概率为
如图,矩形OABC内阴影部分是由曲线f(x)=sinx(x∈(0,π)及直线x=a(a∈(0,π)与x轴围成,向矩形OABC内随机的投掷一点,若落在阴影部分的概率为