Question

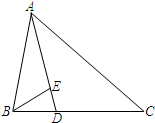如图，在△ABC中，已知∠BAC=

π

3

，AB=2，AC=3，

DC

=2

BD

，

AE

=3

ED

，则|

BE

|=

 

．

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：由向量的运算用向量

AB

和

AC

表示向量

BE

，可得

BE

2的值，由模长公式可得．

解答： 解：∵

DC

=2

BD

，

AE

=3

ED

，
∴

BD

=

1

3

BC

，

AE

=

3

4

AD

，
∴

BE

=

AE

-

AB

=

3

4

AD

-

AB

=

3

4

（

AB

+

BD

）-

AB

=-

1

4

AB

+

3

4

BD

=-

1

4

AB

+

3

4

×

1

3

BC

2
=-

1

4

AB

+

3

4

×

1

3

（

AC

-

AB

）
=-

1

2

AB

+

1

4

AC

∴

BE

2=(-

1

2

AB

+

1

4

AC

)2
=

1

4

AB

2-

1

4

AB

•

AC

+

1

16

AC

2
=

1

4

×22-

1

4

×2×3×

1

2

+

1

16

×32=

13

16

∴|

BE

|=

13

4

故答案为：

13

4

．

点评：本题考查平面向量数量积的运算，涉及平面向量基本定理和模长公式，属中档题．